Integrais definidos no Matlab

Neste tutorial, vou apresentar-lhe o processo de cálculo de integrais definidos no Matlab.

Primeiramente, o que é uma integral definida? Ela permite determinar a área delimitada entre uma função f(x), também designada por função integrando, e o eixo x num intervalo específico (a, b), representado pela notação $$ \int_a^b f(x) \ dx $$.

O Matlab oferece duas funções primordiais para este fim: a função int() e a função quad().

A função int()

Para calcular uma integral definida, o Matlab dispõe da função int(), estruturada da seguinte forma:

int(função, a, b)

Esta função compreende três parâmetros:

• A expressão da função integrando f(x);
• O limite inferior de integração (a);
• O limite superior de integração (b);

Importante salientar que a função int() opera com cálculos simbólicos. Assim, é indispensável definir previamente a variável desconhecida como um símbolo, através da função syms.

Para exemplificar, tomemos a integral

$$ \int_1^2 2x \ dx $$

Neste cenário, temos f(x)=2x como função integrando e o intervalo de integração é (1,2).

Inicialmente, definimos x como símbolo:

syms x

Posteriormente, aplicamos a função int():

int(2*x,1,2)

O resultado, neste caso, é 3.

ans = 3

In this case, the definite integral is equal to 3.

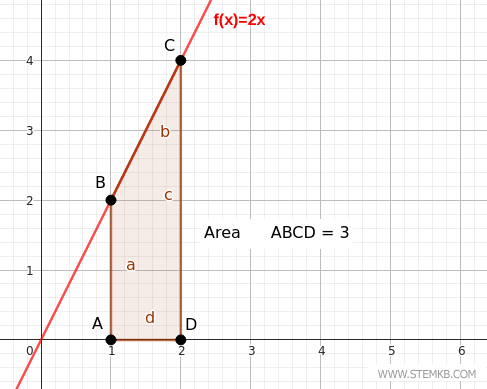
Para validar este cálculo, a integral definida de 2x no intervalo (1,2) pode ser determinada facilmente. $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$ Observando a função num gráfico cartesiano, percebemos que o resultado representa a área entre a curva da função f(x)=2x e o eixo x no intervalo citado.

A função quad()

Para determinar a integral definida de uma função, o Matlab também disponibiliza a função quad().

A sua utilização é bastante intuitiva. A estrutura é:

quad(função, a, b)

Tomando como referência a integral mencionada anteriormente,

$$ \int_1^2 2x \ dx $$

a função integrando é f(x)=2x e o intervalo é (1,2).

Definimos a função de forma anônima:

>> f = @(x) 2*x

E aplicamos a função quad():

>> quad(f,1,2)

Este método estima a área sob o gráfico de f(x)=2x no intervalo (1,2), retornando, neste exemplo, o valor 3.

ans=3

Note-se que o resultado é congruente com o exemplo anterior, onde aplicamos o teorema fundamental do cálculo para resolver a integral. $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$

Diferenças entre int() e quad()

Você pode questionar-se sobre as diferenças entre as funções int() e quad().

Ambas são destinadas ao cálculo de integrais definidos no Matlab, porém fundamentam-se em métodos distintos:

• A função int() emprega métodos numéricos como a regra do trapézio;
• A função quad(), por sua vez, utiliza o método de quadratura adaptativa baseado no algoritmo Gauss-Kronrod, geralmente mais eficiente devido ao menor número de chamadas à função que está sendo integrada.

Em suma, o Matlab é uma ferramenta poderosa para cálculos de integrais, sendo uma referência para engenheiros, físicos e matemáticos.

Com dedicação e prática, você dominará não só as funções quad() e int(), mas também diversos métodos de integração numérica disponíveis na plataforma.