Polinômios no Matlab

Vamos falar sobre polinômios no Matlab.

O que é um polinômio? Polinômios são expressões que consistem em constantes e variáveis, ou monômios, com expoentes inteiros que são combinados utilizando operações aritméticas básicas (adição, subtração, multiplicação e divisão). Por exemplo, este é um polinômio de quarto grau. $$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$ O grau do polinômio é o maior expoente da variável desconhecida x.

Como definir um polinômio no Matlab

Agora, para definir um polinômio no Matlab, vamos considerar este exemplo.

$$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$

O polinômio tem apenas uma variável desconhecida (x).

Para usá-lo no Matlab, você precisa definir um vetor contendo os coeficientes numéricos dos termos.

>> P = [1 2 -1 4 1]

A variável P é um vetor com os coeficientes numéricos do polinômio P(x)=x⁴+2x³-x²+4x+1.

• O primeiro elemento do vetor é o coeficiente 1 de x⁴
• O segundo elemento do vetor é o coeficiente 2 de 2x³
• O terceiro elemento do vetor é o coeficiente -1 de -x²
• O quarto elemento do vetor é o coeficiente 4 de 4x
• O quinto elemento do vetor é o coeficiente 1 de +1

Uma vez criado, você pode usá-lo para calcular os valores do polinômio P(x) variando a variável x usando a função polyval().

Por exemplo, para calcular o valor do polinômio P(x) quando x=0, digite polyval(P,0)

>> polyval(P,0)

O Matlab substitui o valor zero pela variável desconhecida x e retorna o resultado.

Nesse caso, o resultado é 1

ans = 1

Verificação. Você pode verificar rapidamente substituindo x=0 no polinômio $$ P(0) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(0) = (0)^4 + 2 \cdot 0^3 - 0^2 + 4 \cdot 0 +1 $$ $$ P(0)=1 $$ O resultado é 1.

Da mesma forma, você pode calcular o valor do polinômio P(x) quando x=1 digitando polyval(P,1)

>> polyval(P,1)

Nesse caso, o resultado é 7

ans = 7

Verificar. Para verificar o resultado, substitua x=1 no polinômio $$ P(1) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(1) = (1)^4 + 2 \cdot 1^3 - 1^2 + 4 \cdot 1 +1 $$ $$ P(1)=1+2-1+4+1 $$ $$ P(1)=7 $$ O resultado é 7.

Se desejar, também pode calcular o valor do polinômio em uma série de valores de x.

Por exemplo, digite x=0:5 para criar um vetor x com valores de 0 a 5.

>> x=0:5
x =
0 1 2 3 4 5

Agora calcule os valores do polinômio no intervalo de 0 a 5 usando a função polyval(P,x)

>> polyval(P,x)

A função calcula os valores do polinômio para cada elemento no vetor x.

Neste caso, o resultado é um vetor composto por 6 elementos.

ans =
1 7 37 139 385 871

Cada elemento é o valor do polinômio no intervalo (0,5).

Nota. O primeiro elemento do vetor é P(0)=1 quando x=0. O segundo elemento é P(1)=7 quando x=1. O terceiro elemento é P(2)=37. O quarto elemento é P(3)=139. E assim por diante.

O uso de vetores permite realizar cálculos de forma rápida.

Além disso, também permitem representar graficamente o polinômio em um plano cartesiano usando a função plot().

Por exemplo, digite estes comandos em sequência.

>> x=0:5;
>> P = [1 2 -1 4 1] ;
>> y=polyval(P,x);
>> plot(x,y);

O resultado é o gráfico do polinômio no intervalo (0,5).

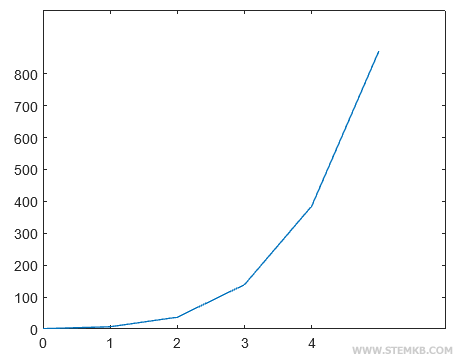
Na eixo horizontal são medidos os valores da variável desconhecida x, enquanto no eixo vertical estão os do polinômio y.

Operações com Polinômios

Você pode usar o Matlab para realizar operações com polinômios.

Vamos a um exemplo prático.

Defina o polinômio x³+2x²+3 no vetor P1

>> P1 = [ 1 2 0 3 ]

Depois, defina o polinômio 2x³-x²+3x+1 no vetor P2

>> P2 = [ 2 -1 3 1 ]

Agora realize as seguintes operações:

Adição

Para somar os dois polinômios, digite P1+P2

>> P1+P2
resposta =
3 1 3 4

O resultado é o polinômio 3x³+x²+3x+4

$$ P_1(x) + P_2(x) = (x^3+2x^2+3) + (2x^3-x^2+3x+1) $$ $$ P_1(x) + P_2(x) = x^3+ 2x^3+2x^2-x^2+3x+1+3 $$ $$ P_1(x) + P_2(x) = 3x^3+x^2+3x+4 $$

Subtração

Para calcular a diferença entre os polinômios, digite P1-P2

>> P1-P2
resposta =
-1 3 -3 2

O resultado é o polinômio -x³+3x²-3x+2

$$ P_1(x) - P_2(x) = (x^3+2x^2+3) - (2x^3-x^2+3x+1) $$ $$ P_1(x) - P_2(x) = x^3- 2x^3+2x^2+x^2-3x+1-3 $$ $$ P_1(x) - P_2(x) = -x^3+3x^2-3x+2 $$

Multiplicação

Para calcular o produto entre os polinômios P1·P2, deve-se utilizar a função de convolução conv()

>> >> conv(P1,P2)
ans =
2 3 1 13 -1 9 3

O resultado é o polinômio 2x⁶+3x⁵+x⁴+13x³-x²+9x+3

$$ P_1(x) \cdot P_2(x) = (x^3+2x^2+3) \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = x^3 \cdot (2x^3-x^2+3x+1) + 2x^2 \cdot (2x^3-x^2+3x+1) + \\ \ \ + 3 \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = 2x^6-x^5+3x^4+x^3 + 4x^5-2x^4+6x^3+2x^2 + \\ \ \ + 6x^3-3x^2+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+(4x^5-x^5)+(3x^4-2x^4)+(x^3 +6x^3+ 6x^3) + \\ \ \ + (2x^2-3x^2)+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+3x^5+x^4+13x^3 -x^2+9x+3 $$

Divisão

Para calcular o quociente de dois polinômios, é necessário utilizar a função de deconvolução deconv()

>> [q,r] = deconv(P1,P2)
q = 0.50000
r = 0.00000 2.50000 -1.50000 2.50000

A função deconv() retorna dois resultados:

• o polinômio do quociente (q)
• o polinômio do resto (r)

O resultado é o polinômio do quociente q=0,5

$$ Q = \frac{1}{2} $$

com resto r=2,5x²-1,5x+2,5

$$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$

Verificação. Realize cálculos algébricos para verificar se o produto está correto. $$ P_1(x) : P_2(x) = \frac{x^3+2x^2+3}{2x^3-x^2+3x+1} $$ Neste caso, o cálculo é um pouco longo.

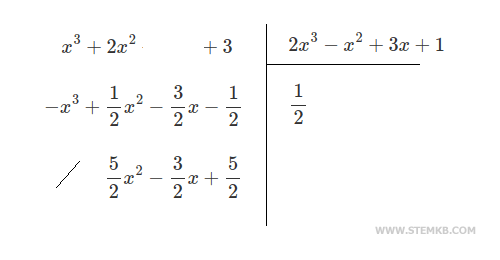
O polinômio do quociente é $$ Q= \frac{1}{2} $$ com resto $$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ Multiplique o quociente pelo polinômio divisor e adicione o resto: $$ Q \cdot (2x^3 -x^2+3x+1) + R $$ $$ \frac{1}{2} \cdot (2x^3 -x^2+3x+1) + \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 - \frac{1}{2} x^2+ \frac{3}{2}x+ \frac{1}{2}+ \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 + \frac{5-1}{2} x^2+ \frac{3-3}{2}x+ \frac{5+1}{2} $$ $$ x^3 + \frac{4}{2} x^2+ \frac{0}{2}x+ \frac{6}{2} $$ $$ x^3 + 2 x^2+ 3 $$ O resultado é o polinômio do dividendo. Portanto, o resultado da divisão entre os dois polinômios está correto.