Funcionalidades da função polyfit() no Matlab
Hoje, vamos explorar uma função extremamente útil no Matlab, conhecida como polyfit(). Essa função é essencial para encontrar um polinômio que se adeque perfeitamente a um conjunto de dados.
polyfit(Y)
O parâmetro dessa função é um array que contém os dados em questão.
Para ilustrar, considere este conjunto de dados:
>> X = [ 1 2 3 4 5 6 ]
>> Y = [ 3 8 6 9 7 8 ]
Esses dados podem ser visualizados em um gráfico através da função plot(X,Y).
>> plot(X,Y)
Este comando gera o gráfico a seguir:
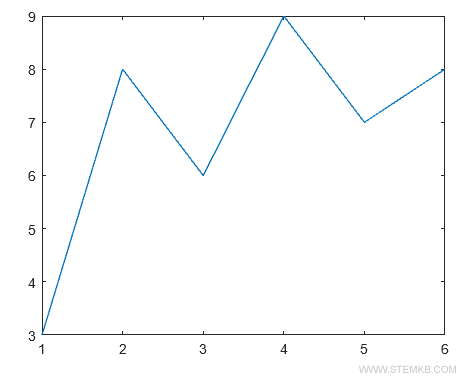
Para obter um polinômio de primeiro grau que se ajuste a esses dados, utilizamos a função polyfit(X,Y,1). Esta função retorna os coeficientes do polinômio de primeiro grau.
>> P = polyfit(X,Y,1)
O resultado obtido é:
P =
0.71429 4.33333
Estes são os coeficientes do polinômio de primeiro grau:
$$ P_1(x) = 0.71429 \cdot x + 4.33333 $$
Com a função polyval(), é possível calcular os valores do polinômio para cada ponto do array X, utilizando como argumento os coeficientes do polinômio e o array X.
>> polyval(P,X)
Essa função calcula os valores do polinômio para cada elemento do array X, gerando o seguinte resultado:
ans =
5.0476 5.7619 6.4762 7.1905 7.9048 8.6190
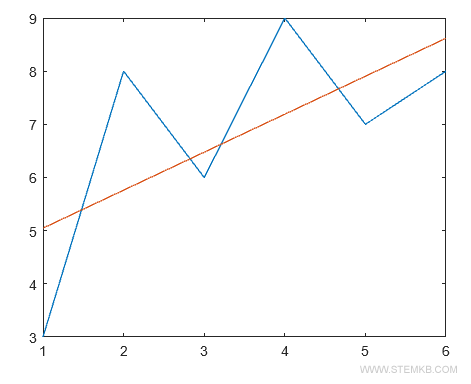
Por fim, é possível exibir os dados e a curva polinomial em um plano cartesiano com a função plot().
plot(X,Y,X,polyval(P,X))
O polinômio linear de primeiro grau fornece uma linha que se aproxima dos dados da série.
Exemplo 2
Suponha agora que você deseja ajustar um polinômio de segundo grau aos dados. A abordagem é semelhante, alterando-se apenas o argumento para 2 na função polyfit().
>> P = polyfit(X,Y,2)
Isso resultará nos coeficientes do polinômio de segundo grau, que podem ser utilizados com a função polyval() para calcular os valores do polinômio para cada elemento do array X.
P =
-0.35714 3.21429 1.00000
Estes são os coeficientes do polinômio de segundo grau.
$$ P_2(x) = -0.35714 \cdot x^2 + 3.21429 x + 1.0 $$
Utilizando a função polyval(P,X), calculamos os valores do polinômio .
>> polyval(P,X)
O resultado é um array com os valores do polinômio para cada ponto do array X.
ans =
3.8571 6.0000 7.4286 8.1429 8.1429 7.4286
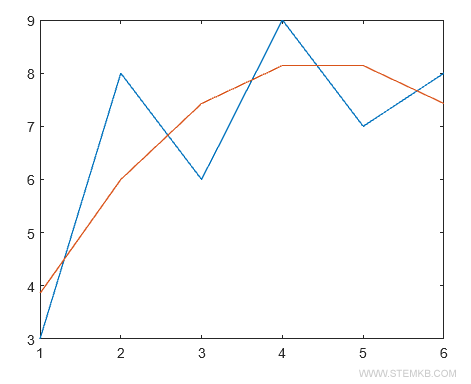
Novamente, ambos os dados e o polinômio podem ser exibidos em um plano cartesiano usando a função plot().
plot(X,Y,X,polyval(P,X))
O polinômio de segundo grau (linha vermelha) se ajusta ainda melhor à série de dados.
Exemplo 3
Por último, o mesmo processo pode ser aplicado para encontrar um polinômio de terceiro grau que se ajuste aos dados.
>> P = polyfit(X,Y,3)
Os resultados da função são:
P =
0.18519 -2.30159 9.08466 -3.66667
Estes são os coeficientes do polinômio de terceiro grau.
$$ P_3(x) = 0.18519x^3 -2.30159 \cdot x^2 + 9.08466 x - 3.66667 $$
A função polyval(P,X) é usada para calcular os valores do polinômio.
>> polyval(P,X)
Assim, obtemos os valores do polinômio para cada ponto do array X.
ans =
3.3016 6.7778 7.8730 7.6984 7.3651 7.9841
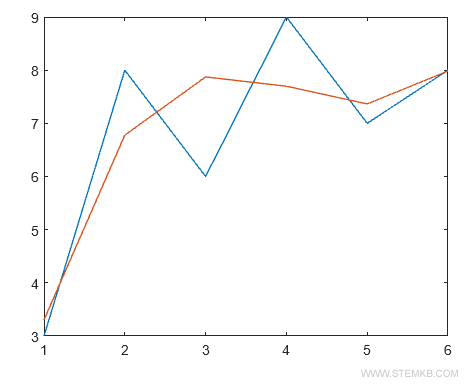
É possível visualizar ambos, dados e polinômio, no diagrama cartesiano com a função plot().
plot(X,Y,X,polyval(P,X))
O polinômio de terceiro grau (linha vermelha) apresenta uma aproximação ainda mais precisa da série de dados.
À medida que aumentamos o grau do polinômio, o erro de aproximação se reduz, proporcionando um ajuste mais preciso à série de dados. Assim, a função polyfit se revela uma ferramenta indispensável para encontrar o polinômio ideal para seus dados no Matlab.