Sistema de equações lineares no Matlab

Nesta aula sobre Matlab, demonstrarei como solucionar um sistema de equações lineares utilizando cálculos matriciais e vetoriais.

Vamos a um exemplo prático.

Este sistema possui duas incógnitas distribuídas em duas equações.

$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$

Observação: Uma equação é considerada linear quando o grau mais elevado de suas incógnitas é 1.

Primeiro, reescrevemos o sistema na forma padrão ax+by=c.

Desloque os termos constantes para o lado direito da equação, mantendo as incógnitas e seus coeficientes à esquerda.

$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$

Converta agora o sistema para a forma vetorial.

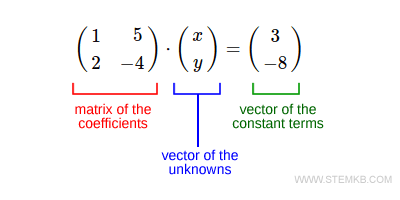
$$ \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

A matriz da esquerda é a matriz dos coeficientes das variáveis desconhecidas x e y.

$$ A = \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} $$

O primeiro vetor representa as incógnitas do sistema.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$

E o último vetor, os termos constantes das equações.

$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

Veja como transpor estas informações para o ambiente do Matlab.

Para definir a matriz de coeficientes no Matlab, insira um array bidimensional.

No terminal, digite A = [1, 5; 2, -4].

>> A = [ 1 , 5 ; 2 , -4 ]
A =
1 5
2 -4

Para o vetor dos termos constantes, insira um array unidimensional.

Digite b = [3; -8].

>> b = [ 3 ; -8 ]
b =
3
-8

O sistema em forma vetorial é resultado do produto de uma matriz por um vetor.

$$ A \cdot \vec{x} = \vec{b} $$

Para solucionar o sistema, isolamos o vetor x, transferindo os demais termos para o lado direito da igualdade.

$$ \vec{x} = A^{-1} \cdot \vec{b} $$

O símbolo A^-1 indica a matriz inversa da matriz de coeficientes A do sistema.

Para calcular A^-1·b no Matlab, utilize o comando inv(B)*b.

>> inv(A)*b
ans =
-2
1

Os resultados representam os valores de x e y no vetor de incógnitas.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$

Com isso, encontramos a solução do sistema de equações.

$$ x=-2 $$

$$ y=1 $$

Portanto, o sistema de equações lineares tem a solução (x;y)=(-2;1).

Confira a correção da solução: Substitua x=-2 e y=1 no sistema original e efetue os cálculos algébricos. $$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$ $$ \begin{cases} -2 + 5 \cdot 1 =3 \\ \\ 2 \cdot (-2) -4 \cdot 1 =-8 \end{cases} $$ $$ \begin{cases} 3 =3 \\ \\ -8 =-8 \end{cases} $$ Como todas as equações se confirmam, a solução x=-2 e y=1 é correta.