Limite de uma Função Usando o Matlab
Hoje, iremos explorar profundamente o intrigante universo dos limites de funções, tirando proveito das robustas capacidades computacionais do Matlab. Vamos não apenas desvendar o conceito, mas também aplicá-lo através de exemplos elucidativos.
Antes de iniciarmos, é crucial esclarecermos o conceito de limites de funções. O limite de uma função representa o valor ao qual essa função se aproxima à medida que sua variável independente converge para um determinado ponto. Para simplificar, ele nos dá uma visão sobre o comportamento da função nas imediações desse ponto específico.
Para começar, introduza 'x', a variável independente, na linha de comando do Matlab, utilizando o comando 'syms'
syms x
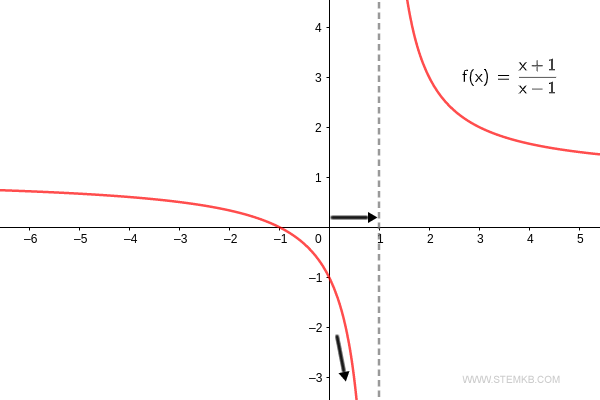
Trabalhemos com a função f(x) = (x+1)/(x-1), onde 'x' é a nossa variável independente. O objetivo é determinar o limite de 'x' ao se aproximar do infinito.
$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$
Posteriormente, você deverá invocar o comando 'limit()'. Defina f(x) como o primeiro argumento, 'x' como o segundo, e 'Inf' (representando o infinito positivo) como o terceiro. Após esta etapa, pressione enter.
limit((x+1)/(x-1),x,Inf)
Imediatamente, o Matlab processa a solicitação e retorna diligentemente o valor limite da função.
ans = (sym) 1
Notadamente, o limite da função, quando 'x' tende ao infinito, é exatamente um.
Contudo, não baseie sua conclusão somente na minha exposição. Como evidenciado, o limite da função f(x) = (x+1)/(x-1) ao se aproximar do infinito é, de fato, um. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$
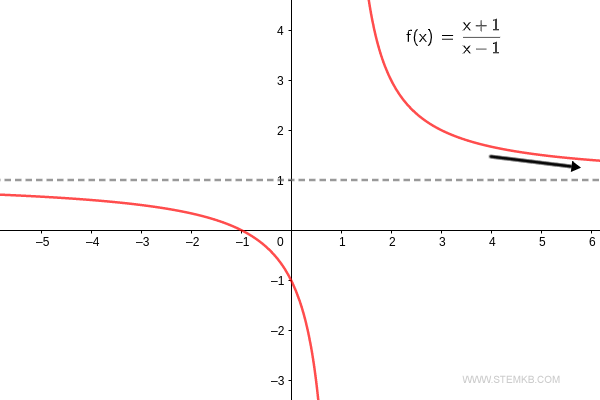
Se estiver interessado em descobrir o limite quando x→-∞, simplesmente inclua '-inf' como o terceiro argumento na função.
limit((x+1)/(x-1),x,-inf)
À medida que 'x' desloca-se em direção ao infinito negativo, a função, contrariamente, ascende em direção ao valor um.
ans = (sym) 1
Reitero, para que não haja dúvidas, que o limite da função f(x) = (x+1)/(x-1) para x→-∞ é incontestavelmente um. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$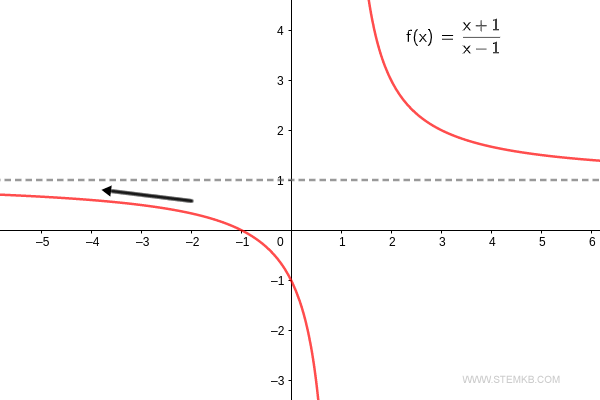
Caso queira determinar o limite da função em um ponto de acumulação específico, 'x0', basta inserir esse ponto como o terceiro parâmetro.
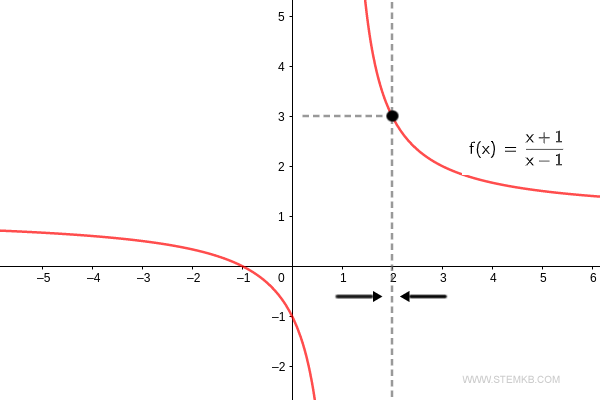
Por exemplo, digamos que estamos buscando o limite da função à medida que 'x' se aproxima de dois.
limit((x+1)/(x-1),x,2)
Aqui, o limite é três.
ans = (sym) 3
Ao conferirmos, vemos que o limite da função f(x) = (x+1)/(x-1) quando x→2 é três. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$
Se estiver interessado apenas no limite pela direita, adicione 'right' como quarto argumento no comando.
limit((x+1)/(x-1),x,1,'right')
O resultado? O limite pela direita da função quando 'x' se aproxima de 1 é infinito positivo ( ∞ ).
ans = (sym) ∞
Só para confirmar, à medida que a função f(x) = (x+1)/(x-1) se aproxima de x=1 pela direita, ela dispara para o infinito positivo. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$
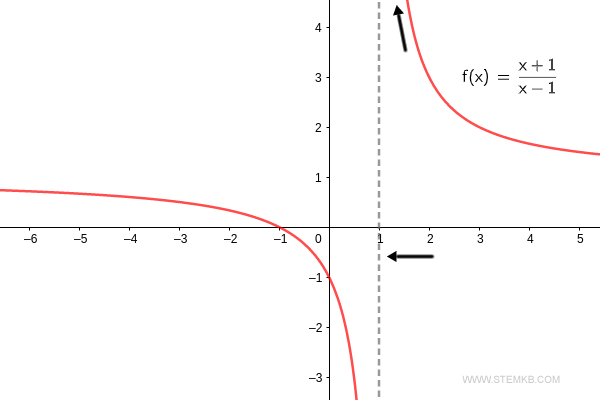
Por outro lado, se o limite pela esquerda for o que você busca, simplesmente adicione 'left' como quarto parâmetro.
limit((x+1)/(x-1),x,1,'left')
E o que encontramos? O limite pela esquerda da função quando 'x' se aproxima de 1 é infinito negativo ( -∞ ).
ans = (sym) -∞
Ao conferir, vemos que o limite pela esquerda da função f(x) = (x+1)/(x-1) para x→1- é realmente o infinito negativo. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$
Com isso, agora você está apto a usar o Matlab para calcular limites de funções.