Vetores no Matlab

Nesta aula, abordaremos como criar um vetor no Matlab.

Comecemos com um exemplo prático.

Imagine um vetor no plano, partindo do ponto (0;0) e estendendo-se até as coordenadas v(2;4).

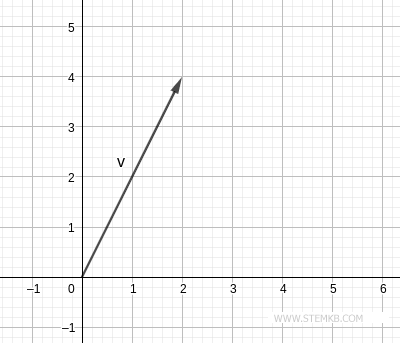
O vetor é composto por duas coordenadas, x=2 e y=4.

Para representá-lo no Matlab, é necessário utilizar uma variável de matriz bidimensional.

Na matriz, as componentes x e y do vetor devem ser separadas por um ponto e vírgula.

>> v=[2;4]

Com isso, define-se um vetor coluna.

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Essa matriz recém-criada pode ser utilizada em diversas operações vetoriais, como adição de vetores, produto vetorial, produto escalar, entre outras.

Criando um Vetor Tridimensional no Matlab

Para formar um vetor com três ou mais componentes, o procedimento é similar.

Considere, por exemplo, um vetor tridimensional no espaço 3D, apontando para as coordenadas v(2;4;3).

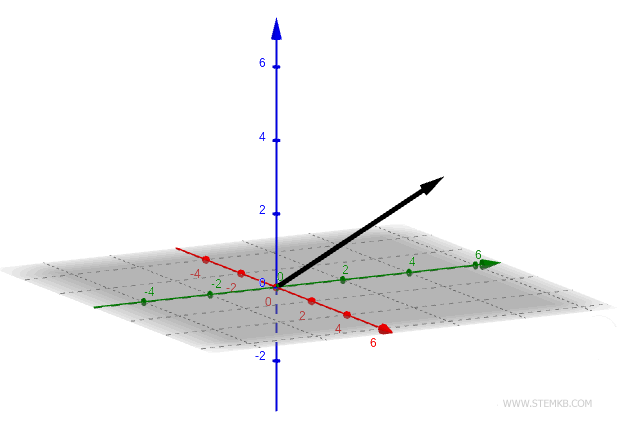
Este vetor possui três componentes: x=2, y=4, z=3.

$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix} $$

Para defini-lo no ambiente Matlab, cria-se uma matriz com os três componentes.

>> v=[2;4;3]

Criando um Vetor Linha

Até o momento, detalhei como criar um vetor coluna, onde os elementos são organizados verticalmente.

$$ \vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$

Para elaborar um vetor linha, com os elementos dispostos horizontalmente, utiliza-se uma sintaxe distinta.

$$ \vec{v} = \begin{pmatrix} a & b & c \end{pmatrix} $$

Para criar um vetor linha no Matlab, forma-se uma matriz e os componentes são separados por um espaço ou vírgula.

Por exemplo, ao definir o vetor linha a seguir:

$$ \vec{v} = \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} $$

Insira uma matriz com os elementos separados por vírgulas.

>> v=[1, 2, 3]

O resultado é um vetor linha.

Nota: Uma alternativa é criar inicialmente um vetor coluna v=[1;2;3] e transformá-lo em vetor linha por meio da transposição de v.