Variáveis Simbólicas no Matlab
No artigo de hoje, abordaremos o tema das variáveis simbólicas no Matlab.
Mas o que exatamente é uma variável simbólica? Trata-se de uma categoria particular de variável que retém unicamente um símbolo, como "x", destinado a cálculos. Ela não conserva um valor numérico fixo. Isso nos permite executar cálculos algébricos simbólicos com um ou mais elementos desconhecidos, tal como resolver equações que contêm duas ou mais variáveis, ou ainda somar dois polinômios.
A definição de uma variável simbólica é feita através da função syms.
Para ilustrar, a variável simbólica "x" pode ser definida da seguinte maneira:
>> syms x
É possível, ainda, definir múltiplas variáveis simbólicas simultaneamente, simplesmente listando-as sequencialmente, separadas por espaços:
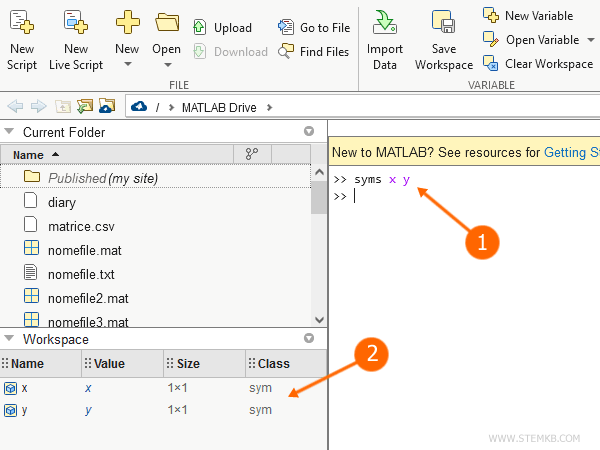
>> syms x y
A cada declaração de uma variável simbólica, ela se torna visível na área de trabalho do Matlab.
Estas variáveis estão vinculadas à classe "sym".
Passemos agora a um exemplo prático.
Considere que temos dois polinômios:
$$ P(x) = 2x + y $$
$$ Q(x) = 4x - 2y $$
E a tarefa é multiplicá-los.
$$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$
Para conduzir tal cálculo algébrico no Matlab, primeiramente definimos as duas variáveis simbólicas "x" e "y" com o comando "syms x y":
>> syms x y
Posteriormente, inserimos a expressão, pq = (2x+y)(4x-2y), na linha de comando.
>> pq = (2*x+y)*(4*x-2*y)
ans =
(4*x - 2*y)*(2*x + y)
O Matlab, reconhecendo "x" e "y" como entidades simbólicas, define de forma automática a expressão simbólica correspondente.
Neste cenário, o Matlab não substitui "x" e "y" por quaisquer valores numéricos, optando por mantê-los como representações simbólicas de variáveis desconhecidas.
Para a resolução algébrica, recorremos à função expand(pq).
>> expand(pq)
ans =
8*x^2 - 2*y^2
O Matlab processa o cálculo de maneira meticulosa, fornecendo-nos o produto resultante dos dois polinômios.
O resultado apresentado é 8x2-2y2
Para verificação da corretude deste, multiplicamos os polinômios manualmente: $$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$ $$ P(x) \cdot Q(x) =2x \cdot 4x + 2x \cdot (-2y) + y \cdot 4x + y \cdot (-2y) $$ $$ P(x) \cdot Q(x) =8x^2 - 4xy + 4xy -2y^2 $$ $$ P(x) \cdot Q(x) =8x^2 -2y^2 $$ Como pode observar, o resultado é, de fato, preciso. Encerramos por aqui nossa discussão de hoje.