Matrizes no Matlab

Nesta lição prática, vamos explorar como definir uma matriz no Matlab, abrangendo tanto matrizes quadradas quanto retangulares.

Aqui vai um exemplo prático para ilustrar.

Primeiro, vamos criar uma matriz quadrada 2x2 com duas linhas e duas colunas.

$$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

Para configurar essa matriz no Matlab, inicie definindo uma variável de array. Insira os elementos da matriz entre colchetes, separando-os por espaços. Um exemplo seria: m = [1 2 3 4].

Posteriormente, delimite as linhas da matriz usando ponto e vírgula (;).

Então, a sintaxe ficaria: m = [ 1 2 ; 3 4 ]

>> m = [ 1 2 ; 3 4 ]

Observação: É possível separar elementos na mesma linha usando espaços (m=[1 2;3 4]) ou vírgulas (m=[1,2;3,4]). Ambos os métodos produzem o mesmo resultado. No entanto, é recomendável usar espaços para uma melhor visualização dos pontos e vírgulas que separam as linhas. O uso de vírgulas pode reduzir a legibilidade, especialmente em matrizes com elementos decimais.

Com isso, o Matlab cria um array de duas linhas e duas colunas com os elementos especificados.

E assim obtemos a matriz quadrada 2x2

m =
1 2
3 4

Depois de criar a matriz, ela está pronta para ser utilizada em diversas operações matriciais.

Exemplo: No Matlab, é possível realizar várias operações com a matriz, como calcular seu determinante, posto, a soma ou o produto com outras matrizes, além de encontrar a inversa ou a transposta. Por exemplo, para calcular o determinante da matriz m, basta digitar det(m).

Definição de matrizes retangulares no Matlab

O procedimento para criar matrizes retangulares segue a mesma lógica.

Por exemplo, para definir uma matriz retangular 3x4 com três linhas e quatro colunas:

$$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{pmatrix} $$

Para esta tarefa no Matlab, você deve escrever uma variável de array com 12 elementos.

Separando os elementos por espaços ou vírgulas, delimite as linhas com ponto e vírgula.

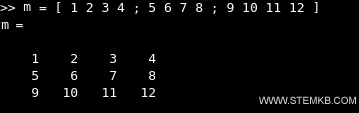
>> m = [ 1 2 3 4 ; 5 6 7 8 ; 9 10 11 12 ]

Isso resulta em um array bidimensional (linhas e colunas) de 12 elementos, organizados em três linhas e quatro colunas.

Obtemos, assim, a matriz retangular 3x4.

Com esses passos, é possível definir qualquer matriz, seja ela quadrada ou retangular, com o número desejado de linhas e colunas, em duas dimensões.