Matriz esparsa no Octave

Nesta aula online, tenho o prazer de lhes ensinar como criar uma matriz esparsa utilizando o Octave.

Você deve estar se perguntando, o que é uma matriz esparsa e para que serve? Bem, quando criamos uma matriz de grande porte com uma quantidade considerável de zeros, acabamos por ocupar desnecessariamente um amplo espaço na memória do computador. Vamos tomar como exemplo uma matriz diagonal, que contém valores não nulos apenas na diagonal principal, sendo os demais elementos zeros. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Podemos alcançar o mesmo efeito ao criar uma matriz esparsa, na qual os zeros são compactados, resultando em um uso mais eficiente da memória.

Matrizes esparsas são excelentes ferramentas para a criação de matrizes identidade e matrizes diagonais compactadas.

A matriz de identidade esparsa

Vamos explorar um pouco mais isso com um exemplo prático.

Para criar uma matriz de identidade, basta digitar o comando eye(4)

>> eye(4)
ans =
Diagonal Matrix1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Essa matriz contém 12 zeros e 4 uns. É evidente que uma grande parcela do espaço é ocupada desnecessariamente por valores nulos.

Agora, se usarmos a técnica da matriz esparsa com o comando speye(4), poderemos criar a mesma matriz identidade:

>> speye(4)
ans =
Compressed Column Sparse (rows = 4, cols = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

Observe que a matriz esparsa só armazena as posições (linha, coluna) onde existem valores não nulos, economizando espaço na memória.

Essa é a razão pela qual ela recebe o nome de "esparsa" (sparse matrix).

É importante salientar que a matriz esparsa armazena apenas as informações relevantes. Em uma matriz identidade, os valores nulos são, de fato, irrelevantes. Portanto, eles são eliminados, otimizando o espaço de memória utilizado e acelerando os cálculos da matriz. Esse benefício é ainda mais notável quando estamos lidando com matrizes de grande porte.

Essa matriz esparsa recém-criada pode ser utilizada em seus cálculos da mesma forma que uma matriz de identidade 4x4.

Por exemplo, vamos criar uma matriz com 4 colunas.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Agora, vamos multiplicar a matriz M pela matriz de identidade.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Em seguida, multiplicamos a matriz M pela matriz de identidade esparsa.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Como se pode ver, o resultado é o mesmo em ambos os casos.

Contudo, no segundo caso, você utilizou menos memória e reduziu o tempo de cálculo.

A Matriz Diagonal Esparsa

Você pode criar uma matriz diagonal esparsa com valores diferentes de 1 usando o comando spdiags()

>> spdiags([1;2;3],0,3,3)
ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

• O primeiro parâmetro é um vetor coluna [1; 2; 3] com os elementos da diagonal.
• O segundo parâmetro é o índice da diagonal, onde o número zero (0) é a diagonal principal.
• Os terceiro e quarto parâmetros são o número de linhas (3) e colunas (3) da matriz esparsa.

O resultado é uma matriz esparsa 3x3 com elementos na diagonal principal.

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Defina uma matriz esparsa indicando apenas os valores não nulos

É possível criar uma matriz esparsa especificando apenas os valores não nulos e suas posições na matriz.

Por exemplo, vamos criar uma matriz esparsa com os seguintes valores:

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Para isso, definimos um vetor com tantas linhas quantos forem os valores não nulos.

Em cada linha do vetor, escrevemos o número da linha, o número da coluna e o valor do elemento não nulo.

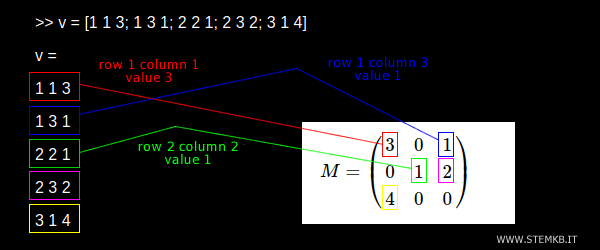
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Observação: o primeiro elemento não nulo (3) está na primeira linha e coluna (1,1). Portanto, a primeira linha do vetor é 1 1 3. O segundo elemento não nulo (1) está na primeira linha e terceira coluna. Assim, a segunda linha do vetor é 1 3 1. O terceiro elemento não nulo (2) está na segunda linha e segunda coluna, o que nos leva a definir a terceira linha do vetor como 2 2 2, e assim por diante.

Agora, para criar a matriz esparsa, utilizamos a função spconvert()

>> spconvert(v)

O resultado é uma matriz esparsa com os valores nas posições que você especificou.

ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

No array usado para construir a matriz esparsa, você pode definir os valores não nulos em qualquer ordem.

Nota. Você também pode indicar vários valores para a mesma posição na matriz. Quando uma posição no array está presente várias vezes no array, o Octave soma os valores sem dar erro. Por exemplo, defina uma matriz esparsa indicando na posição (1,1) o valor 2 e o valor 3. Na posição (1,1) o Octave soma os dois valores 2 + 3 = 5

Com este método, você também pode criar uma matriz esparsa com números complexos.