A rotação de uma matriz no Octave
Nesta aula, vamos desvendar o processo de rotação de uma matriz no Octave, ilustrado com exemplos práticos para facilitar a compreensão.
Primeiramente, o que significa rotacionar uma matriz? Imagine que a matriz gira como um ponteiro de relógio: para a direita (sentido horário) ou para a esquerda (sentido anti-horário). Por exemplo, ao rotacionar a matriz 90° no sentido horário, obtemos o seguinte resultado:
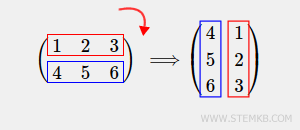
Vamos começar criando uma matriz retangular 2x3
>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6
Agora, vamos girar a matriz 90° no sentido anti-horário.
Digite rot90(M,1)
>> rot90(M,1)
ans =
3 6
2 5
1 4
O que temos aqui é a matriz inicial rotacionada 90° para a esquerda.
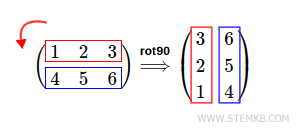
Vale ressaltar que para obter este resultado, você também pode simplesmente digitar rot90(M), pois o Octave assume por padrão o segundo parâmetro igual a 1. A direção padrão é anti-horária (para a esquerda), uma convenção comum em matemática e física. Para girar a matriz para a direita, você deve indicar um número negativo. Por exemplo, -1.
Se deseja girar a matriz 90° para a direita, digite rot90(M, -1).
Neste caso, o segundo parâmetro é um número inteiro negativo, ou seja, -1.
>> rot90(M,-1)
ans =
4 1
5 2
6 3
Desta vez, o resultado é a matriz girada 90° para a direita.
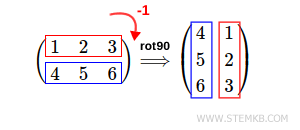
Você também pode girar a matriz 180° para a esquerda.
Para isso, você deve digitar rot90(M,2)
>> rot90(M,2)
ans =
6 5 4
3 2 1
O resultado é uma dupla rotação de 90° da matriz para a esquerda.
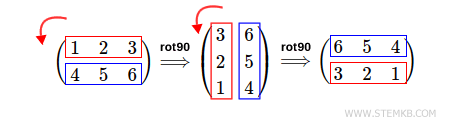
Da mesma forma, você pode girar a matriz 180° para a direita digitando rot90(M, -2).
Neste caso, o segundo parâmetro é um número inteiro negativo, ou seja, -2.
>> rot90(M,-2)
ans =
6 5 4
3 2 1
O resultado é uma dupla rotação de 90° da matriz para a direita.
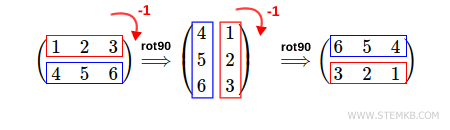
Você pode realizar qualquer número de rotações da matriz usando a função rot90(M, n).
O segundo parâmetro indica o número de rotações para a esquerda (n> 0) ou para a direita (n <0).
Por exemplo, para girar a matriz 270° para a esquerda, digite rot90(M,3)
>> rot90(M,3)
ans =
4 1
5 2
6 3
O resultado é a matriz girada três vezes 90° para a esquerda.
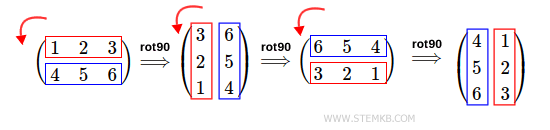
Note que para girar a matriz 270° para a direita, basta digitar rot90(M, -3), indicando -3 como o segundo parâmetro da função.
Para girar a matriz 360° para a esquerda, digite rot90(M,4)
>> rot90(M,4)
ans =
1 2 3
4 5 6
Neste caso, você obtém a mesma matriz inicial, pois realizou quatro rotações de 90° para a esquerda.
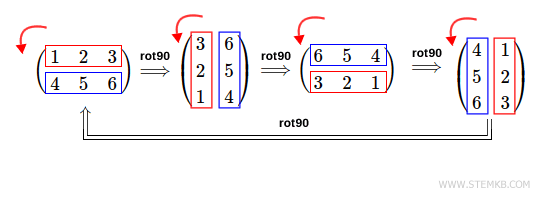
Espero que esta aula tenha ajudado a esclarecer o processo de rotação de matrizes no Octave.
Lembre-se, a prática leva à perfeição, então continue experimentando com diferentes rotações e observe os resultados.