A transposição de uma matriz no Octave

No decorrer desta aula, irei orientá-los sobre o processo de transposição de uma matriz utilizando o Octave.

Antes de mergulharmos diretamente, vamos entender: o que é uma matriz transposta? Em essência, a transposição de uma matriz envolve a conversão de cada linha em uma coluna, e reciprocamente. Por exemplo, considere uma matriz M que possui duas linhas e três colunas.

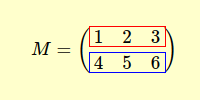
A matriz transposta M^T é formada ao dispor os elementos de cada linha de M nas colunas.

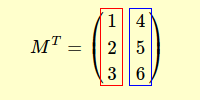
Vamos colocar essa teoria em prática com um exemplo.

Inicialmente, crie uma matriz retangular que contém seis elementos.

>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6

Esta matriz é constituída por duas linhas e três colunas.

$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$

Para obter a matriz transposta, digite o nome da variável seguido de um apóstrofo, ou seja, M'

>> M'
ans =
1 4
2 5
3 6

Como alternativa, você pode transpor a matriz digitando transpose(M)

>> transpose(M)
ans =
1 4
2 5
3 6

Em ambos os cenários, a matriz resultante é a matriz transposta.

A matriz transposta resultante é uma matriz retangular 3x2, com as linhas agora rearranjadas em colunas.

$$ M^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$

Vale a pena ressaltar: a primeira linha da matriz original, composta pelos elementos [1 2 3], agora representa a primeira coluna da matriz transposta. O mesmo se aplica à segunda linha da matriz original. A segunda linha [4 5 6] da matriz original torna-se a segunda coluna da matriz transposta.