Como substituir as diagonais de uma matriz no Octave

Nesta lição, vou ensinar a substituir os elementos de uma diagonal em uma matriz.

Primeiro, vamos entender o que são as diagonais de uma matriz. Elas são compostas pelos elementos que se estendem do canto superior direito ao inferior esquerdo e vice-versa. Por exemplo, na matriz M, a diagonal principal é formada pelos elementos 1, 5, 9.$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Vamos a um exemplo prático.

Crie uma matriz 3x3:

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

A diagonal principal é composta pelos elementos 1, 5, 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Para substituir os elementos da diagonal principal por -1, -2, -3, utilize o comando spdiags([-1;-5;-9],0,M)

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• O primeiro parâmetro é um vetor coluna [-1;-5;-9] com os novos elementos da diagonal.
• O segundo parâmetro (0) é o índice da diagonal, sendo que a diagonal principal tem índice 0.

  Nota. Índice 1 é a diagonal acima da diagonal principal enquanto índice -1 é a diagonal abaixo.

• O terceiro parâmetro M é a variável onde a matriz é armazenada.

O resultado é uma matriz quadrada com os novos elementos na diagonal principal.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Para alterar os elementos na diagonal acima da diagonal principal, utilize o comando spdiags([-1;-5;-9],1,M)

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

A função substitui os elementos acima da diagonal principal.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

Note que o primeiro elemento -1 do vetor coluna [-1;-5;-9] não aparece na nova matriz, pois está fora dela.

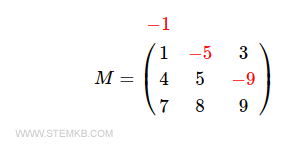
Para substituir elementos na diagonal secundária, combine as funções spdiags() e fliplr()

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

A função substitui os valores na diagonal secundária da matriz, que começa no canto superior direito e termina no canto inferior esquerdo.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

Assim, é possível substituir todos os valores nas diagonais secundárias da matriz.