Substituição de diagonais em matrizes no Matlab

Neste tutorial, explicarei como substituir elementos nas diagonais de uma matriz utilizando o Matlab, uma ferramenta essencial para manipulação matricial.

O que são as diagonais de uma matriz? Refere-se aos elementos alinhados transversalmente, formando linhas que se estendem do canto superior direito ao inferior esquerdo, ou o inverso. Por exemplo, a diagonal principal da matriz M inclui os elementos 1, 5 e 9. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Apresentarei um exemplo prático para melhor compreensão.

Como criar uma matriz quadrada 3x3 com três linhas e três colunas:

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

A diagonal principal desta matriz é formada pelos elementos 1, 5 e 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Para substituir os elementos da diagonal principal, utilize o comando spdiags([-1;-5;-9],0,M) na linha de comando do Matlab. Isso substituirá os elementos da diagonal principal pelos números -1, -5 e -9.

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• O primeiro parâmetro, um vetor coluna [-1;-5;-9], contém os novos elementos a serem inseridos na diagonal da matriz.
• O segundo parâmetro (0) indica o índice da diagonal a ser modificada. No caso, 0 corresponde à diagonal principal.
• O terceiro parâmetro, M, é o nome da variável que armazena a matriz.

Este comando altera a matriz, substituindo os elementos originais da diagonal principal pelos novos valores.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Para modificar os elementos da diagonal acima da principal, execute o comando spdiags([-1;-5;-9],1,M).

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

Esse comando atualiza os elementos imediatamente acima da diagonal principal da matriz.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

Nota: O elemento -1 do vetor coluna [-1;-5;-9] não aparece na matriz modificada, pois está fora do seu alcance. Assim, somente -5 e -9 são inseridos.

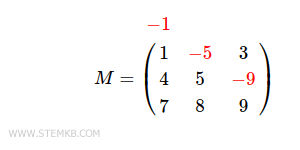
E sobre a substituição dos elementos na diagonal secundária?

A diagonal secundária se inicia no canto superior direito e termina no inferior esquerdo.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{3} \\ 4 & \color{red}{5} & 6 \\ \color{red}{7} & 8 & 9 \end{pmatrix} $$

Para alterar os elementos na diagonal secundária, é necessário utilizar as funções spdiags() e fliplr().

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

A função fliplr() espelha a matriz horizontalmente.

$$ \text{ fliplr }(M) = \begin{pmatrix} 3 & 2 & 1 \\ 6 & 5 & 4 \\ 9 & 8 & 7 \end{pmatrix} $$

Em seguida, a função spdiags() substitui os valores na diagonal principal da matriz espelhada.

$$ \text{ fliplr }(M) = \begin{pmatrix} \color{red}{-1} & 2 & 1 \\ 6 & \color{red}{-5} & 4 \\ 9 & 8 & \color{red}{-9} \end{pmatrix} $$

Consequentemente, na matriz original M, os elementos da diagonal secundária são substituídos.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

Com esses comandos, é possível também modificar valores em outras diagonais da matriz.

Nota: Para ajustar as diagonais acima e abaixo da secundária, varie o índice na função spdiags() para 1 ou -1. Por exemplo, para alterar os elementos acima da diagonal secundária, use o comando
fliplr(spdiags([-1;-5;-9],1,fliplr(M))). Isso resultará em: $$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ \color{red}{-9} & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$ Para modificar os elementos abaixo da diagonal secundária, utilize o comando
fliplr(spdiags([-1;-5;-9],-1,fliplr(M))). O resultado será: $$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & \color{red}{-1} \\ 7 & \color{red}{-5} & 9 \end{pmatrix} $$