Extração da diagonal de uma matriz em Matlab
Nesta lição, vou demonstrar como se pode extrair os elementos da diagonal de uma matriz utilizando o Matlab.
O que é a diagonal de uma matriz? A diagonal principal de uma matriz é formada pelos elementos situados na diagonal que se estende do canto superior esquerdo ao inferior direito. A título de exemplo, na matriz a seguir, os elementos da diagonal principal, destacados em vermelho, são 1, 5 e 9. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Vamos a um exemplo prático.
Comece criando uma matriz quadrada 3x3 com três linhas e três colunas, preenchida com os seguintes elementos.
>> M=[1 2 3; 4 5 6; 7 8 9]
M =
1 2 3
4 5 6
7 8 9
Para extrair os elementos da diagonal principal, utilize a função diag(M).
>> diag(M)
ans =
1
5
9
Esta função seleciona os elementos da diagonal principal da matriz, que neste exemplo são 1, 5 e 9.
$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
A função diag() também permite acessar outras diagonais da matriz.
Para extrair os elementos da diagonal acima da principal, por exemplo, utilize diag(M,1).
>> diag(M,1)
ans =
2
6
Nesse caso, diag(M,1) retorna os números 2 e 6, localizados na diagonal imediatamente acima da principal.
$$ M = \begin{pmatrix} 1 & \color{red}2 & 3 \\ 4 & 5 & \color{red}6 \\ 7 & 8 & 9 \end{pmatrix} $$
Experimente agora a função diag(M,2).
>> diag(M,2)
ans = 3
Com este comando, são extraídos os elementos da diagonal que se encontra uma linha acima da anterior.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$
Para obter as diagonais abaixo da principal, basta inserir um número inteiro negativo como segundo parâmetro.
Por exemplo, diag(M,-1) extrai os elementos da diagonal situada abaixo da principal.
>> diag(M,-1)
ans =
4
8
Assim, diag(M,-1) seleciona os elementos 4 e 8, localizados abaixo da diagonal principal.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ \color{red}4 & 5 & 6 \\ 7 & \color{red}8 & 9 \end{pmatrix} $$
Para transformar a matriz original em uma matriz diagonal, mantendo apenas os elementos da diagonal principal, utilize diag(diag(M)).
>> diag(diag(M))
ans =
Matriz Diagonal
1 0 0
0 5 0
0 0 9
Desta forma, obtem-se uma matriz diagonal.
$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{pmatrix} $$
Como extrair a diagonal secundária?
A diagonal secundária, ou antidiagonal, é formada pelos elementos que vão do canto superior direito ao inferior esquerdo da matriz.
Para a matriz 3x3 do exemplo, a diagonal secundária inclui os elementos 3, 5 e 7.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Para acessar a diagonal secundária, primeiro é necessário inverter a matriz horizontalmente com a função fliplr(). Em seguida, use a função diag().
Por exemplo, execute diag(fliplr(M)) para obter os elementos da diagonal secundária.
>> diag(fliplr(M))
ans =
3
5
7
Com diag(fliplr(M)), os elementos 3, 5 e 7 da diagonal secundária são extraídos.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Nota: Também é possível usar o segundo parâmetro da função diag() para extrair diagonais acima ou abaixo da diagonal secundária. Inserindo um inteiro positivo, como em diag(fliplr(M),1), obtêm-se os elementos 2 e 4, que estão logo acima da diagonal secundária. $$ M = \begin{pmatrix} 1 & \color{red}2 & \color{green}3 \\ \color{red}4 & \color{green}5 & 6 \\ \color{green}7 & 8 & 9 \end{pmatrix} $$ Utilizando um inteiro negativo, como em diag(fliplr(M),-1), extrai-se os elementos 6 e 8, localizados logo abaixo da diagonal secundária.
$$ M = \begin{pmatrix} 1 & 2 & \color{green}3 \\ 4 & \color{green}5 & \color{red}6 \\ \color{green}7 & \color{red}8 & 9 \end{pmatrix} $$ .
A função diag() é essencial para extrair elementos das diagonais, inclusive em matrizes retangulares.
Imagine, por exemplo, a criação de uma matriz retangular 3x4, com 3 linhas e 4 colunas.
>> M2=[1 1 1 1 ; 2 2 2 2 ; 3 3 3 3]
M2 =
1 1 1 1
2 2 2 2
3 3 3 3
Para isso, utilize o comando diag(M2).
>> diag(M2)
ans =
1
2
3
Este comando, diag(M2), é capaz de capturar os elementos situados na diagonal, percorrendo da esquerda para a direita, iniciando pelo elemento no canto superior esquerdo.
$$ M = \begin{pmatrix} \color{red}1 & 1 & 1 & 1 \\ 2 & \color{red}2 & 2 & 2 \\ 3 & 3 & \color{red}3 & 3 \end{pmatrix} $$
Assim, você pode extrair qualquer diagonal, independentemente de a matriz ser quadrada ou não.
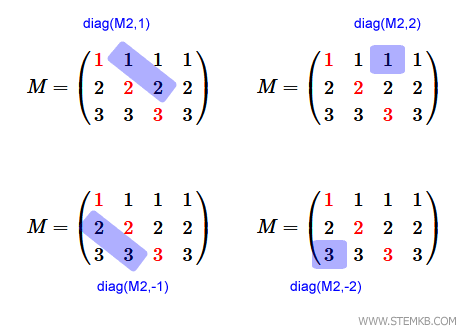
Observação: Nas matrizes retangulares, também é possível extrair diagonais acima ou abaixo da principal, utilizando um inteiro positivo ou negativo como segundo parâmetro. Por exemplo, para acessar as diagonais acima e abaixo da principal, utilize diag(M2,1) e diag(M2,-1), respectivamente. Da mesma forma, diag(M2,2) e diag(M2,-2) permitem acessar as diagonais subsequentes.
Para extrair as diagonais secundárias de uma matriz retangular, é necessário inverter a matriz da direita para a esquerda. Nesse caso, para obter a diagonal secundária, digite diag(fliplr(M2)). Aqui, a diagonal secundária inicia no elemento mais à direita do topo da matriz retangular. $$ M = \begin{pmatrix} 1 & 1 & 1 & \color{red}1 \\ 2 & 2 & \color{red}2 & 2 \\ 3 & \color{red}3 & 3 & 3 \end{pmatrix} $$