Matrizes esparsas no Matlab

Neste tutorial, vou mostrar como criar matrizes esparsas utilizando o Matlab de forma eficiente.

O que são matrizes esparsas? Matrizes esparsas são fundamentais para manipular grandes conjuntos de dados com eficácia, aproveitando melhor a memória do computador. Imagine criar uma matriz com muitos valores repetidos, como zeros, por exemplo. Essa repetição acaba consumindo uma quantidade significativa de memória desnecessariamente. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Para otimizar o uso da memória, podemos representar essa mesma matriz de forma esparsa, onde os valores nulos são simplificados, reduzindo assim o espaço ocupado.

Com o Matlab, é possível criar matrizes identidade e diagonais esparsas, otimizando seus cálculos e armazenamento.

Matriz identidade esparsa

Vamos a um exemplo prático:

Crie uma matriz identidade com a função eye(4).

>> eye(4)
ans =
Matriz Diagonal
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Observamos que nesta matriz, 12 dos 16 elementos são zeros, o que indica um uso excessivo de memória para esses valores repetidos.

Agora, vamos criar a mesma matriz no formato esparsa com o comando speye(4).

>> speye(4)
ans =
Matriz Esparsa Comprimida (linhas = 4, colunas = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

Nesta representação, o Matlab lista apenas as posições (linha, coluna) com valores não nulos, economizando memória significativamente.

Por isso, denominamos essa estrutura como matriz "esparsa".

Note que a matriz esparsa é mais eficiente em termos de memória, pois leva em conta apenas as informações relevantes. Em matrizes identidade, por exemplo, os zeros não contribuem para os cálculos e, portanto, são eliminados, diminuindo tanto a complexidade espacial quanto a temporal.

Essa matriz esparsa pode ser usada em cálculos da mesma forma que uma matriz normal.

Por exemplo, considere uma matriz quadrada M de quatro linhas e colunas.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Agora, multiplique M por uma matriz identidade de tamanho 4.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Em seguida, multiplique a mesma matriz M por uma matriz identidade esparsa de tamanho 4.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Os resultados das operações M*eye(4) e M*speye(4) são idênticos. Contudo, a operação com a matriz esparsa é mais rápida e eficiente em termos de uso da memória.

Matriz diagonal esparsa

O Matlab também oferece uma função específica para criar matrizes diagonais esparsas: spdiags().

spdiags(v,i,r,c)

• O primeiro parâmetro (v) é um vetor coluna contendo os elementos da diagonal
• O segundo (i) indica o índice da diagonal (por padrão, 0 para a diagonal principal)
• Os terceiros e quartos parâmetros (r e c) definem o número de linhas e colunas da matriz esparsa

Por exemplo, utilize spdiags([1;2;3],0,3,3) para criar uma matriz diagonal esparsa 3x3.

>> spdiags([1;2;3],0,3,3)
ans =
Matriz Esparsa Comprimida (linhas = 3, colunas = 3, nnz = 3 [33%])
(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

Aqui, o Matlab posiciona os elementos [1;2;3] na diagonal principal de uma matriz 3x3, resultando numa matriz esparsa eficiente.

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Como criar manualmente uma matriz esparsa

No Matlab, você também pode definir uma matriz esparsa listando a posição de cada valor não nulo na matriz.

Por exemplo, crie uma matriz esparsa baseada nesta matriz

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Escreva a lista de valores não nulos da matriz em um array, especificando a linha, a coluna e o valor.

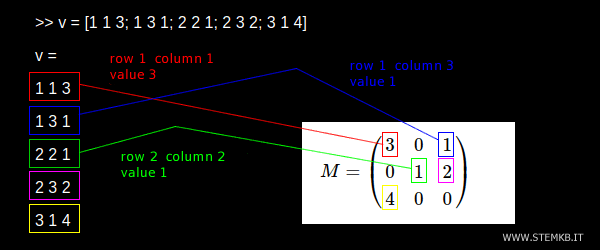
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Cada linha do array indica a posição (linha e coluna) e um valor de um elemento não nulo da matriz.

O primeiro elemento não nulo (3) da matriz está localizado na primeira linha e primeira coluna (1,1). Ele é o elemento escrito em vermelho no exemplo abaixo. Para indicar este elemento na lista da matriz esparsa, você precisa escrever 1 1 3 em uma linha do array. E assim por diante.

Depois de definir o array com a lista de valores não nulos, crie a matriz esparsa usando a função spconvert().

>> spconvert(v)

O resultado é uma matriz esparsa com os valores nas posições que você indicou.

ans =
Matriz Esparsa de Coluna Comprimida (linhas = 3, colunas = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

Ao criar o array, você pode definir os elementos não nulos da matriz em qualquer ordem.

Você também pode indicar a mesma posição da matriz várias vezes com valores diferentes.

Observe que se você definir a mesma posição na matriz várias vezes em um array, o Matlab somará todos os valores. Por exemplo, se você criar uma matriz esparsa indicando o valor 2 e o valor 3 na posição (1,1), o Matlab considerará a soma dos dois valores como 2+3=5 na posição (1,1) da matriz.

Este método também permite que você gere uma matriz esparsa com números complexos.