Limites de funções no Octave

Deseja aprender a calcular o limite de uma função no Octave? Neste guia, apresentaremos alguns exemplos práticos para auxiliá-lo.

Pré-requisitos. É essencial que você já tenha o software GNU Octave instalado em seu computador, juntamente com o módulo Symbolic.
Além disso, familiarize-se com a interface gráfica do Octave para uma melhor experiência.

Primeiramente, defina a variável independente x como símbolo da função.

Utilize o comando syms na linha de comando do Octave:

syms x

Vamos calcular o limite de x tendendo ao infinito ( x→∞) para a função f(x)=(x+1)/(x-1)

$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$

Digite o comando limit()

Insira o nome da função f(x) no primeiro parâmetro e o nome da variável x no segundo.

limit((x+1)/(x-1),x)

O Octave calcula o limite da função quando x→∞

ans = (sym) 1

Neste caso, o limite da função é 1.

O limite da função f(x)=(x+1)/(x-1) quando x→∞ é 1. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ 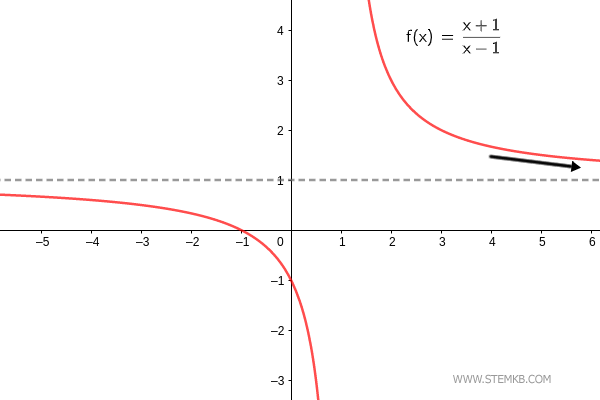o gráfico da função com x tendendo ao infinito

Se o seu objetivo é determinar o limite quando x tende a menos infinito ( x→-∞ ), o procedimento é semelhante.

Basta adicionar `-inf` como terceiro parâmetro:

limit((x+1)/(x-1),x,-inf)

O resultado, neste caso, também é 1.

ans = (sym) 1

O limite da função f(x)=(x+1)/(x-1) quando x→-∞ é 1. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$ 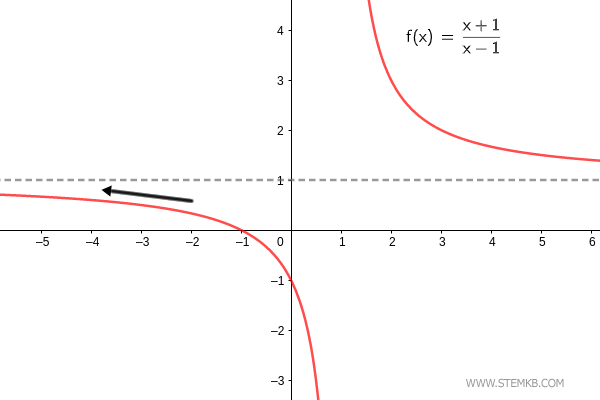o gráfico da função com x tendendo a menos infinito

Para avaliar o limite em um ponto específico, como x = 2, indique o valor desejado no terceiro parâmetro:

limit((x+1)/(x-1),x,2)

O resultado para este exemplo é 3.

ans = (sym) 3

O limite da função f(x)=(x+1)/(x-1) quando x→2 é 3. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ 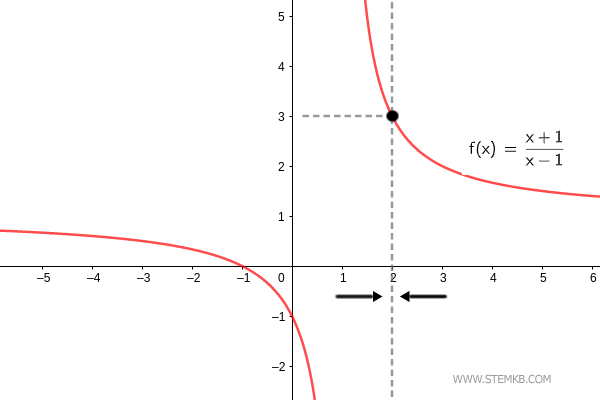o limite da função com x tendendo a 2

Se quiser calcular apenas o limite à direita, use o mesmo comando e digite 'right' no quarto parâmetro.

limit((x+1)/(x-1),x,1,'right')

O resultado é infinito (∞).

ans = (sym) ∞

O limite da função f(x)=(x+1)/(x-1) quando x→1⁺ é infinito. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ 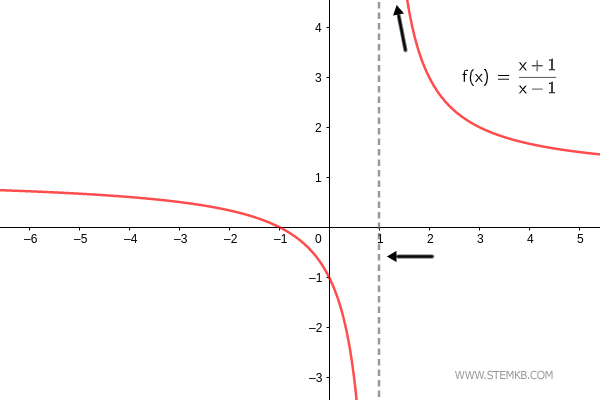o limite à direita da função quando x se aproxima de um

Para calcular o limite à esquerda, use o mesmo comando e digite 'left' no quarto parâmetro.

limit((x+1)/(x-1),x,1,'left')

O resultado é menos infinito (-∞).

ans = (sym) -∞

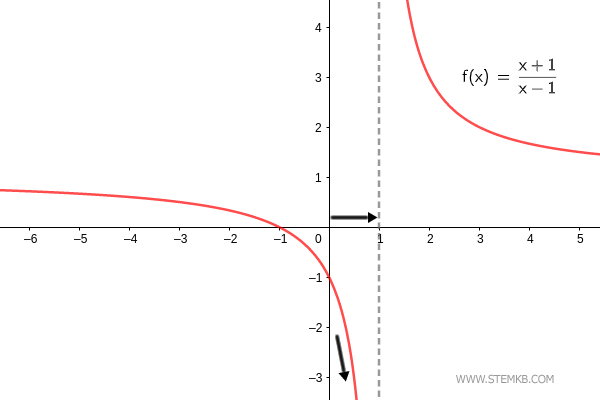
O limite da função f(x)=(x+1)/(x-1) quando x→1^- é menos infinito. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$
o limite à esquerda da função quando x se aproxima de um

Esperamos que este guia tenha sido esclarecedor. Se encontrou utilidade e deseja aprofundar seus conhecimentos em Octave, continue nos acompanhando.