Criação de gráficos em degraus no Matlab
Hoje vamos explorar o Matlab e nos aprofundar nos gráficos em degraus, uma ferramenta interessante e bastante útil.
O que são, afinal, esses gráficos em degraus? Pense no gráfico de uma função, mas, ao invés de uma linha suave e contínua, ele apresenta uma sequência de degraus. Esses gráficos são perfeitos para ilustrar variações discretas nos valores de uma função.
Iniciemos com um exemplo simples.
Imagine que possuímos um vetor 'x', variando de 1 a 20.
>> x=linspace(1,20,20);
Este vetor 'x' constitui o domínio de nossa função.
Em seguida, criamos um vetor 'y' que representará os valores da nossa função y=f(x).
>> y=x
Ao executarmos plot(x,y), obtemos o gráfico de y=f(x).
>> plot(x,y)
O resultado é uma linha contínua que vai de 1 a 20, caracterizando-se por uma reta que cruza a origem.
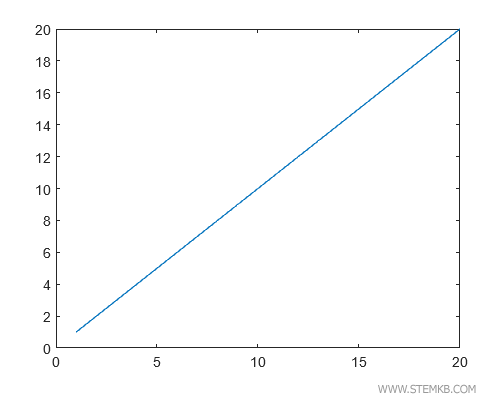
Mas agora, vamos adicionar mais dinâmica ao processo. Utilize stairs(x,y) para gerar um gráfico em degraus.
>> stairs(x,y)
A função stairs(x,y) nos permite conectar pontos adjacentes através de degraus, em vez de uma linha ininterrupta.
O resultado? Um diagrama de degraus bastante informativo.
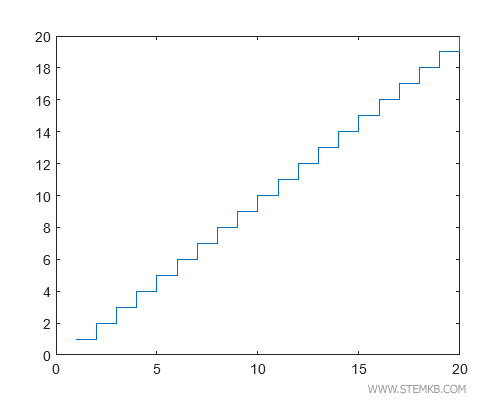
Neste exemplo, os degraus são uniformes, refletindo o aumento constante da função linear em cada intervalo.
Avançando para um exemplo mais complexo.
Definamos a função y=x2, que calcula o quadrado de cada valor de x.
y=x.^2
O gráfico contínuo desta função revela uma curva exponencial.
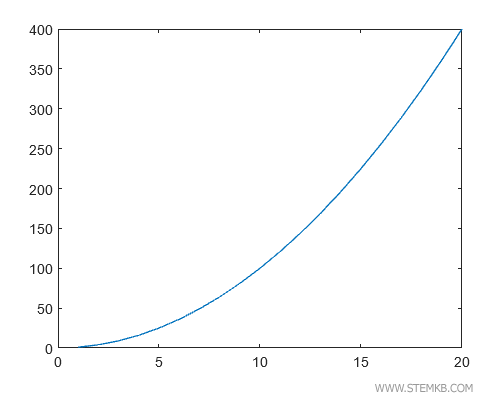
Contudo, ao aplicarmos stairs(x,y) para formar o diagrama em degraus...
>> stairs(x,y)
...obtemos um gráfico composto por degraus de alturas variadas, onde cada degrau mais elevado indica um ponto de maior crescimento da função.
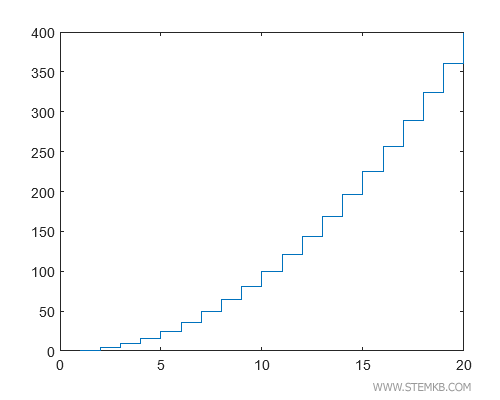
Aqui, os degraus aumentam de altura à medida que o valor de x cresce, demonstrando um crescimento mais acentuado da função.
Como exibir vários gráficos em um único diagrama?
Se você deseja comparar duas funções no mesmo gráfico, isso é perfeitamente viável.
Por exemplo, crie um vetor Y com dois elementos.
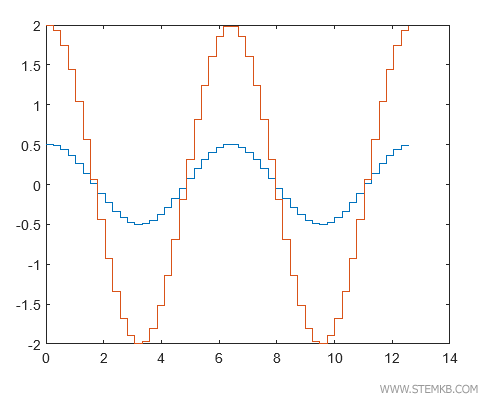
Considere 0.5cos(X) como o primeiro elemento e 2cos(X) como o segundo.
>> X = linspace(0,4*pi,50)';
>> Y = [0.5*cos(X), 2*cos(X)];
Executando stairs(Y) ou stairs(X,Y), ambos os gráficos em degraus são exibidos simultaneamente.
>> stairs(X,Y)
Pronto! Agora temos um diagrama cartesiano único, mostrando os gráficos em degraus de ambas as funções, facilitando a comparação entre elas.

E se quiser ir além, é possível exibir três ou mais funções no mesmo gráfico. Basta definir um vetor com três ou mais elementos e seguir o procedimento.