Gráfico de degraus no Octave
Nesta aula, vou orientá-lo sobre como elaborar um gráfico de degraus no Octave, passo a passo.
Mas o que é, exatamente, um gráfico de degraus? Trata-se de um gráfico onde a função é representada de forma discreta, com saltos que se assemelham a degraus, não sendo, portanto, contínuo. Este tipo de gráfico é particularmente útil para evidenciar variações no incremento da função.
Permita-me ilustrar com um exemplo prático.
Inicialmente, crie um vetor, x, da variável independente com valores de 1 a 20.
>> x=linspace(1,20,20);
Em seguida, crie um vetor para uma função linear.
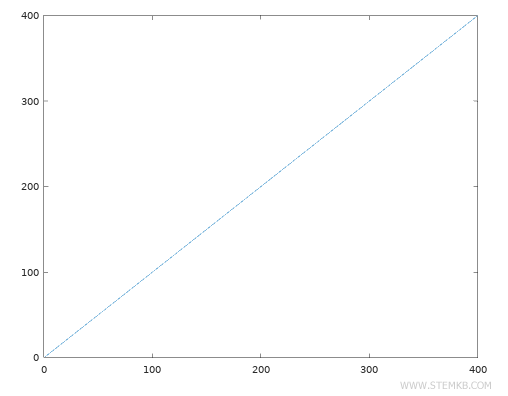
>> y=x
Agora, trace a função utilizando a função plot(x,y).
>> plot(x,y)
O gráfico resultante da função y = f(x) = x é uma linha simples que passa pela origem.
Para criar um gráfico de degraus, utilize a função stairs(x, y).
>> stairs(x,y)
O diagrama resultante apresenta o mesmo gráfico, porém em formato de degraus.
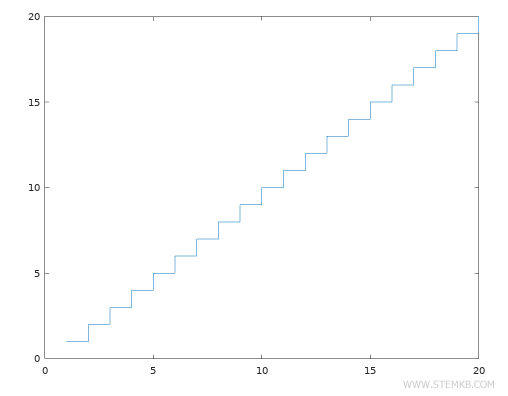
Os degraus são todos iguais, indicando que a função tem uma taxa de crescimento constante.
Permita-me ilustrar com outro exemplo prático
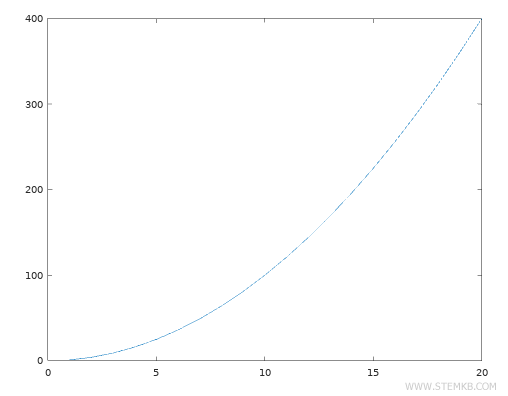
Crie uma função y = x^2.
y=x.^2
Trace a função utilizando a instrução plot(x,y)
Neste caso, a função cresce de forma exponencial.
Utilize o comando stairs(x, y) para desenhar o diagrama de degraus da função.
>> stairs(x,y)
O diagrama de degraus mostra degraus de diferentes alturas.
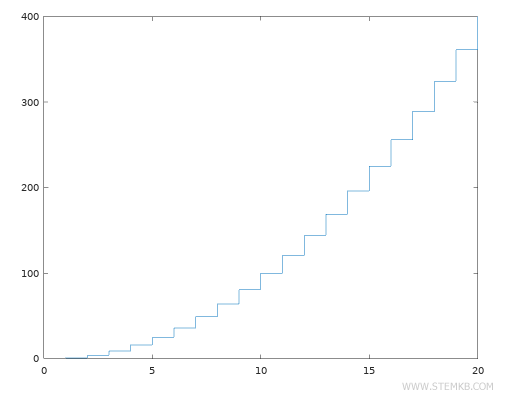
Os últimos degraus são mais altos, indicando que a função tem uma taxa de crescimento que tende a aumentar.
Como exibir múltiplos gráficos em um único diagrama?
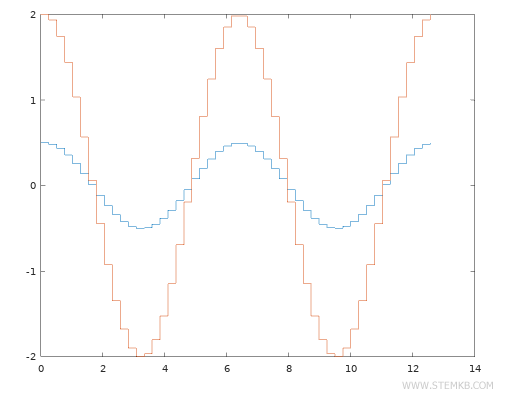
Para exibir dois gráficos de degraus no mesmo diagrama, indique as duas funções em uma matriz Y com duas colunas.
>> X = linspace(0,4*pi,50)';
>> Y = [0.5*cos(X), 2*cos(X)];
A primeira coluna da matriz Y representa os valores da função 1/2*cos(X), e a segunda coluna representa os valores da função 2*cos(x).
Agora, exiba o gráfico utilizando o comando stairs(Y) ou stairs(X, Y).
>> stairs(X,Y)
Desta forma, os gráficos de degraus de ambas as funções são exibidos no mesmo diagrama.

Se você achou esta aula útil, continue nos acompanhando.