Cálculo da norma de um vetor no Matlab

Nesta aula, explicarei como se calcula a norma (ou magnitude) de um vetor utilizando o Matlab.

O que é a norma de um vetor? Refere-se ao comprimento euclidiano do vetor, também conhecido como sua magnitude. A norma euclidiana de um vetor no plano, por exemplo, corresponde ao comprimento da seta que o representa.

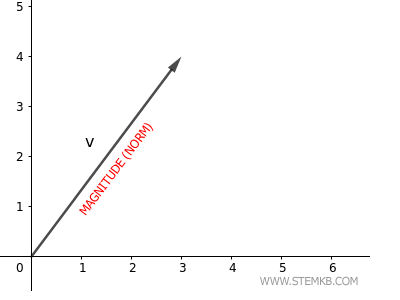
Para ilustrar, vejamos um exemplo prático.

Considere um vetor na variável V

>> V=[3 4]
V =
3 4

Este vetor tem origem no ponto (0;0) do plano e se estende até o ponto (3;4).

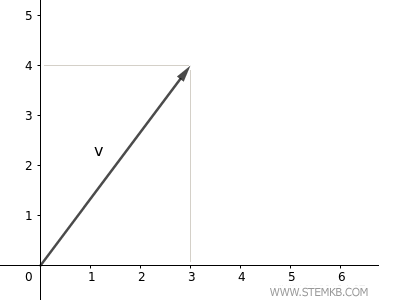
Para calcular o comprimento do vetor (sua magnitude ou norma), utiliza-se a função norm(V).

>> norm(V)
ans = 5

A norma euclidiana do vetor, neste caso, é 5.

Este valor representa o comprimento da seta que simboliza o vetor no plano.

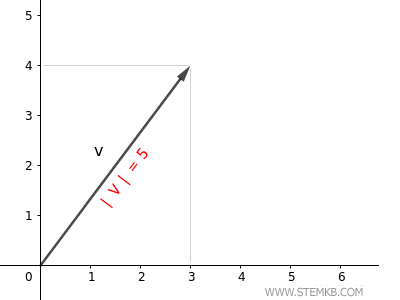
Verificação. O comprimento de um vetor também pode ser calculado aplicando-se o teorema de Pitágoras $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ De fato, a magnitude do vetor é 5, confirmando a exatidão do resultado obtido.