Como determinar o comprimento de um vetor no Octave

Nesta lição, vou mostrar como calcular o comprimento de um vetor usando o Octave.

Mas o que é, exatamente, o comprimento de um vetor? Trata-se do seu comprimento euclidiano, também conhecido como norma. Para simplificar, a norma euclidiana de um vetor equivale ao comprimento da seta que representa esse vetor no espaço.

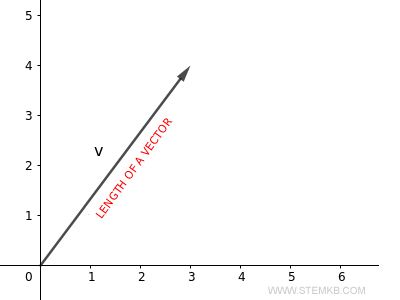
Agora, vou apresentar um exemplo prático para esclarecer.

Primeiramente, definimos um vetor na variável V, assim:

>> V=[3 4]
V =
3 4

Temos aqui um vetor cujo ponto final é (3;4).

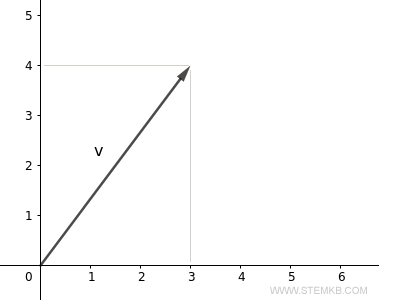
Agora, para determinar o comprimento desse vetor (ou seja, a sua magnitude ou norma), utilizamos a função norm(V), como segue:

>> norm(V)
ans = 5

Com isso, descobrimos que o comprimento do nosso vetor (ou norma) é igual a 5.

Este é o comprimento da seta representada no plano cartesiano.

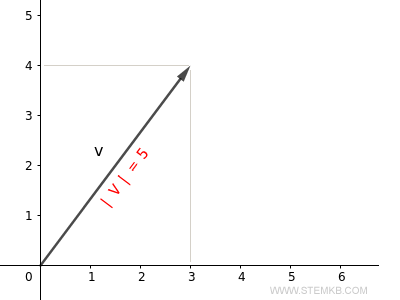
Para confirmar, podemos calcular o comprimento do vetor (ou módulo) usando o teorema de Pitágoras: $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ Conforme calculado, o comprimento do vetor é 5. O resultado é, portanto, correto.