Ângulo e módulo de um número complexo em Octave

Nesta lição, vou explicar como calcular o ângulo (argumento) e o módulo de um número complexo no Octave.

O que são o módulo e o ângulo de um número complexo? Todo número complexo z = a + bi pode ser representado no plano complexo nas coordenadas (a, b).

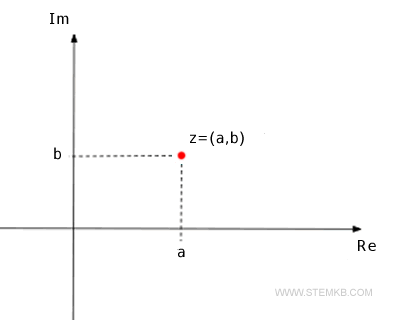
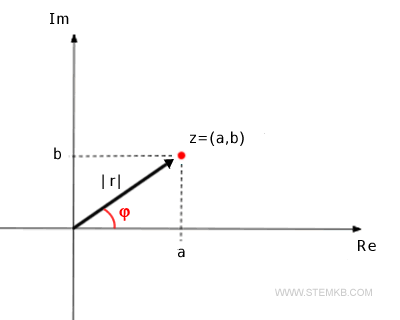
Assim, cada ponto no plano é um número complexo diferente e pode ser alcançado de forma única a partir da origem por meio de um vetor. O comprimento r = |z| do vetor é chamado de módulo do número complexo z. O ângulo φ do vetor medido no sentido anti-horário a partir do eixo real positivo (Re) é chamado de argumento do número complexo.

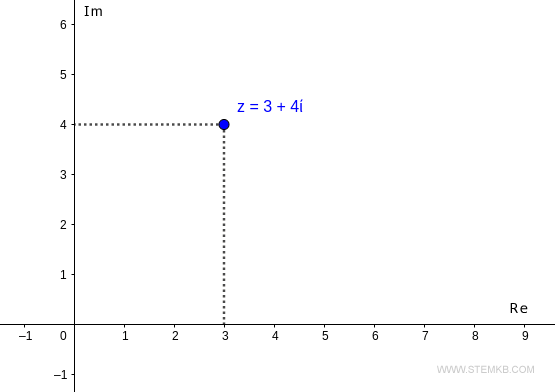
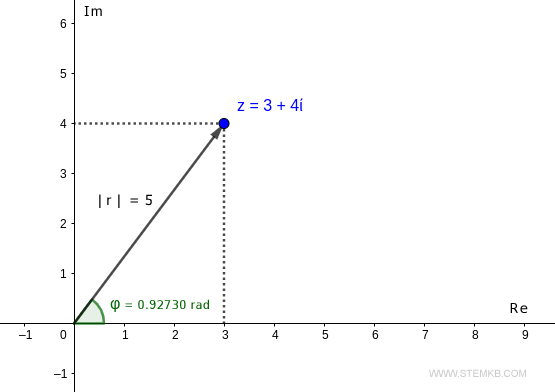
Por exemplo, considere o número complexo z=3+4i

No plano complexo, o número z está localizado no ponto com coordenadas (3,4).

Este ponto é alcançável a partir da origem por apenas um vetor de comprimento r e ângulo φ.

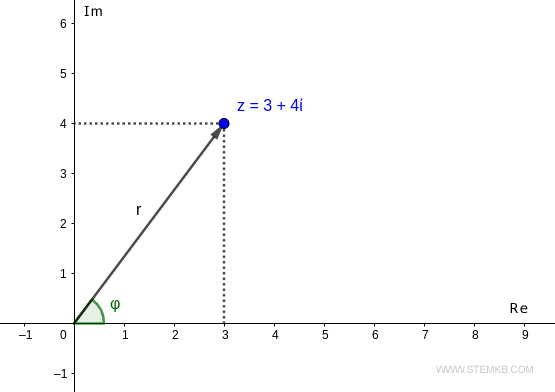
Para calcular o módulo r = |z| do número complexo, que é o comprimento do vetor, use a função abs() no Octave.

>> abs(z)
ans= 5

Portanto, o módulo do número complexo z = 3 + 4i é igual a 5.

Em outras palavras, o vetor que conecta a origem com o ponto (3,4) tem comprimento de cinco.

Para calcular o ângulo (argumento) do número complexo, use em vez disso a função angle().

>> angle(z)
ans = 0.92730

O Octave retorna o ângulo em radianos.

Neste caso, o argumento do número complexo z = 3 + 4i é 0,92730 radianos, que é aproximadamente 53 graus.

Se esta lição sobre Octave por Nigiara foi útil, continue a nos