Conjugado complexo em Octave
Nesta lição, vou explicar como encontrar o conjugado de um número complexo no Octave.
O que é o conjugado complexo? O conjugado de um número complexo z = a + bi é um número complexo que tem a mesma parte real e a parte imaginária mudada de sinal. Por exemplo, o número complexo z1 = 2 + 3i tem como conjugado complexo z2 = 2-3i, e vice-versa.
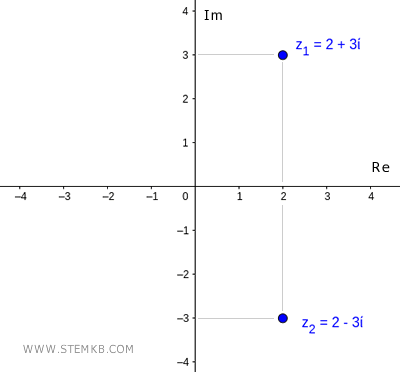
Aqui está um exemplo prático.
Defina o número complexo z = 2 + 3i no Octave usando a função complex(2,3).
>> z=complex(2,3)
ans = 2 + 3i
Para obter o conjugado de um número complexo no Octave, você pode usar a função conj().
Por exemplo, se você tiver um número complexo z = 2 + 3i, pode encontrar seu conjugado digitando conj(z)
>> conj(z)
ans = 2 - 3i
A função retornará o conjugado do número complexo, que neste caso é 2-3i.
Qual é o objetivo de calcular o conjugado complexo?
O cálculo do conjugado complexo simplifica certas operações na aritmética de números complexos.
Por exemplo, o produto de um número complexo com seu conjugado é igual ao quadrado de sua magnitude.
Para calcular, multiplique o número complexo z por seu conjugado conj(z). O produto é igual a 13.
>> z*conj(z)
ans = 13
Para calcular o módulo do número complexo z, você pode usar a função embutida abs() no Octave.
O resultado da aplicação desta função a z é aproximadamente 3,6.
>> abs(z)
ans = 3.6056
Além disso, calcule o quadrado do módulo de z.
O resultado sempre será 13.
>> (abs(z))^2
ans = 13.000
Isso implica que o módulo de um número complexo também pode ser obtido tirando a raiz quadrada do produto do número complexo e seu conjugado.
>> sqrt(z*conj(z))
ans = 3.6056
Se você achou a lição de Nigiara útil para usar números complexos no Octave, certifique-se de continuar seguindo-nos para mais.
Nota. No contexto de números complexos, "magnitude" e "modulus" são frequentemente usados indistintamente para se referir ao valor absoluto ou à distância de um número complexo da origem do plano complexo.