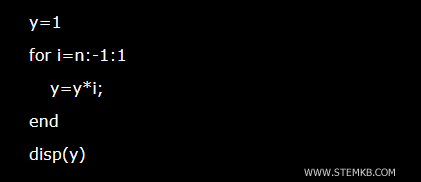Funções recursivas no Octave
Nesta lição, vou explicar como usar a recursão em funções no Octave.
Recursão refere-se à técnica de uma função se chamando múltiplas vezes. É um conceito fundamental na programação funcional.
Para ajudá-lo a entender esse conceito, vou fornecer um exemplo prático.
Você pode usar a recursão para calcular o fatorial de um número.
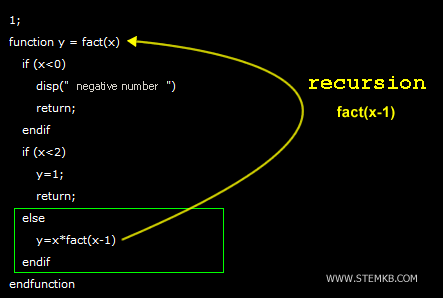
1;
function y = fact(x)
if (x<0)
disp("negative number")
return;
endif
if (x<2)
y=1;
return;
else
y=x*fact(x-1)
endif
endfunction
Neste script, eu defini uma função chamada facr() que recebe uma entrada numérica (x).
- Se x<0
Em primeiro lugar, a função verifica se a entrada é negativa. Se x<0, a função exibe uma mensagem dizendo que o número é negativo e termina a chamada da função usando a declaração return. Isso ocorre porque o fatorial de um número negativo é indefinido.

- Se 0≤x<2
Em seguida, a função verifica se a entrada é menor que 2. Se 0≤x<2, a função retorna 1 e termina a recursão. A declaração return envia o valor 1 de volta para a chamada de função anterior, efetivamente fechando o loop recursivo.

- Se x≥2
Por fim, se a entrada for maior ou igual a 2, a função multiplica o número de entrada x pelo resultado de fact(x-1). Isso é alcançado por meio da recursão, onde a função se chama com uma nova entrada de x-1, que é o número inteiro atual x reduzido por um. O processo se repete até que o caso base de x<2 seja alcançado e a recursão termine.
Em geral, essa função fornece uma maneira eficiente de calcular fatoriais de números inteiros não negativos.
Por exemplo, você pode chamar a função fact() que você acabou de criar e passar 6 como parâmetro inicial.
n=6
y=fact(n);
disp(y)
O script retorna o número 720, que é o fatorial de 6!
720
Por que a saída da função é 720?
A função se chama cinco vezes (recursão) passando um número progressivamente menor.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
Na última chamada fact(1)=1, a função retorna 1 porque o valor de entrada (x=1) é menor que dois.
Nesse ponto, a recursão termina e o processo retorna para trás, fechando todas as chamadas anteriores.
Se fact(1)=1 então fact(2)=2 porque fact(2)=2*fact(1)=2*1=2
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
Se fact(2)=2 então fact(3)=6 porque fact(3)=3*fact(2)=3*2=6
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
Se fact(3)=6 então fact(4)=24 porque fact(4)=4*fact(3)=4*6=24
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
Se fact(4)=24 então fact(5)=120 porque fact(5)=5*fact(4)=5*24=120
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
Se fact(5)=120 então fact(6)=720 porque fact(6)=6*fact(5)=6*120=720
fact(6)=6*fact(5)=6*120=720
Portanto, o fatorial de 6! é 720.
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Observação. Neste exemplo, criei uma função fatorial para explicar como a recursão funciona no Octave. No entanto, se você precisa apenas calcular o fatorial, lembre-se de que o Octave também possui uma função pré-definida específica, factorial(x), que é muito mais conveniente de usar. Além disso, você pode calcular o fatorial desenvolvendo uma função baseada em iteração sem usar a recursão, e o resultado será sempre o mesmo.