Cálculo de integrais com o GeoGebra

No tutorial de hoje, vamos explorar como calcular a integral indefinida de uma função utilizando o GeoGebra, por meio de um exemplo prático e detalhado.

Primeiramente, o que é uma integral indefinida? Integrar uma função, como f(x), significa encontrar outra função, g(x)+k, $$ \int f(x) = g(x) + k $$ onde, ao derivarmos D[g(x)+k], retornamos à função original f(x). $$ D_t[ g(x) + k ] = f(x) $$

Para começar, insira uma função no GeoGebra. Neste exemplo, usaremos f(x)=x².

Em seguida, utilize o comando Integral().

No interior dos parênteses do comando, indique a função a ser integrada, que, para este exemplo, foi denominada "f".

O GeoGebra efetuará o cálculo e mostrará a integral indefinida como g(x)=1/3·x³ para a função f(x) selecionada.

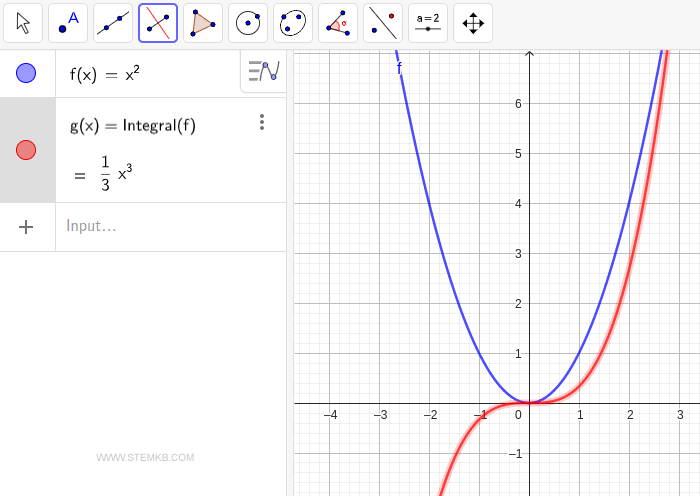
É importante salientar que o resultado de uma integral indefinida não se resume a uma única função g(x), mas representa uma família de funções, g(x)+k, em que k é uma constante arbitrária. Assim, uma maneira mais precisa de expressá-la seria g(x)=1/3·x³+k. Esse conceito se apoia no fato de que a derivada de qualquer constante k é zero, portanto D[k] = 0. Consequentemente, derivadas como D[1/3·x³+2] ou D[1/3·x³+3] sempre nos levarão de volta à função original f(x)=x².

Quer verificar?

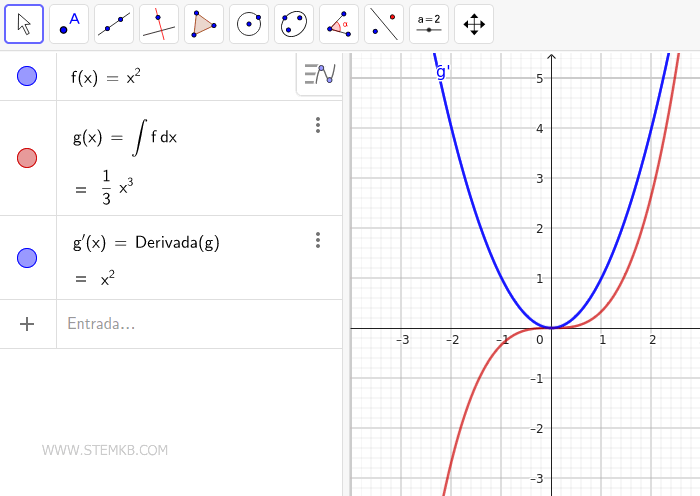
Confirme seus resultados calculando a derivada com o comando Derivada().

Aplicando a derivada a g(x)=1/3·x³, obtemos novamente a função inicial f(x)=x², reafirmando que a diferenciação é o processo inverso da integração.

Se este guia foi útil para você, convidamos a descobrir mais em nossos próximos tutoriais.