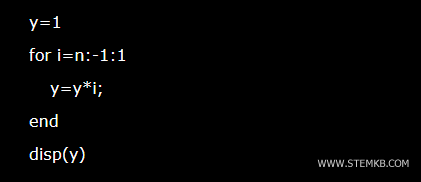Funções recursivas no Matlab
Recentemente, estive aprofundando meus conhecimentos sobre funções recursivas no Matlab e gostaria de compartilhar algumas reflexões sobre o assunto.
O que é recursão? Em essência, uma função recursiva é aquela que se autoinvoca uma ou mais vezes. Este conceito, essencial na programação funcional, revela-se extremamente útil na resolução de problemas específicos.
Vamos a um exemplo prático:
Imagine que você deseja calcular o fatorial de um número (n!). Uma abordagem seria definir uma função recursiva desta forma:
function y = fact(x)
if (x<0)
disp("número negativo")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end
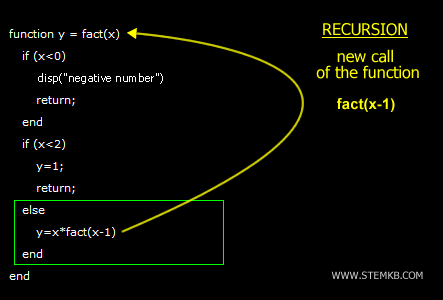
A função fact(), nesse contexto, é um exemplo clássico de função recursiva, pois ela se chama na expressão y = x * fact(x - 1).
Explicando seu funcionamento:
Primeiramente, a função fact() recebe um número x. Vejamos o processo:
- Se x<0
Caso x seja negativo, a função cessa sua execução, pois o fatorial de um número negativo não existe. A função então exibe "número negativo" e interrompe a execução com o comando return.

- Se 0≤x<2
Para x positivo e menor que 2, a função retorna 1, finalizando a recursão sem novas autoinvocações. O comando return passa o valor 1 para a chamada recursiva anterior, encerrando assim o ciclo.

- Se x≥2
Com x maior ou igual a 2, a função realiza a operação x vezes fact(x - 1), invocando-se recursivamente.
Por exemplo, ao chamar a função fact() com x = 6, o processo seria:
n=6;
y=fact(n);
disp(y)
function y = fact(x)
if (x<0)
disp("número negativo")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1 );
end
end
Observação: Uma função em Matlab deve ser sempre definida ao final do script.
A função processa o valor de entrada x = 6 e inicia o cálculo do fatorial de 6! de maneira recursiva.
A função é invocada 5 vezes (recursão), reduzindo o número a cada chamada.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
Na última invocação, fact(1) = 1, a função retorna 1, finalizando as chamadas recursivas anteriores.
Assim, se fact(1) = 1, então fact(2) = 2, pois fact(2) = 2 * fact(1) = 2 * 1 = 2.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
E seguindo essa lógica, se fact(2) = 2, então fact(3) = 6, já que fact(3) = 3 * fact(2) = 3 * 2 = 6, e assim sucessivamente.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
Portanto, com fact(3) = 6, fact(4) será 24, pois fact(4) = 4 * fact(3) = 4 * 6 = 24, e assim por diante.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
Concluímos que fact(5) é 120, e consequentemente, fact(6) será 720.
fact(6)=6*fact(5)=6*120=720
E assim se desvenda o mistério!
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Logo, o fatorial de 6 é 720.
720
Observação: Embora neste exemplo tenhamos criado uma função recursiva para calcular o fatorial de um número, é importante lembrar que, no Matlab, você também pode utilizar a função predefinida factorial(x) para obter o mesmo resultado sem a necessidade de definir uma função adicional.
factorial(6)=720
Alternativamente, é possível calcular o fatorial de um número por meio de uma função iterativa, sem recorrer à recursão. De qualquer forma, o resultado final será sempre o mesmo.
Veja um exemplo de algoritmo para calcular o fatorial usando iteração: