Produto vetorial no Geogebra

Neste tutorial, vou guiá-lo através do processo de cálculo do produto vetorial entre dois vetores utilizando o Geogebra.

Inicie criando dois vetores num espaço tridimensional.

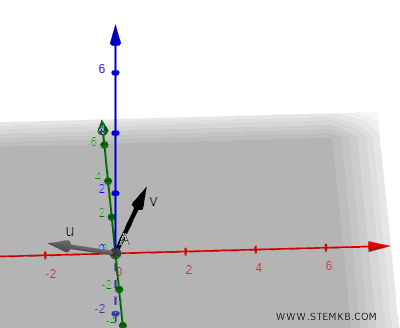
Para o primeiro vetor, as coordenadas são

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

Quanto ao segundo vetor,

$$ \vec{u} = \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} $$

Caso tenha dúvidas sobre como criar um vetor, nossa lição online "Criar vetores com o Geogebra" pode ajudar.

A seguir, insira o comando ProdutoVetorial(v,u) no campo de comandos do Geogebra e pressione enter.

Nesse contexto, u e v são os nomes dos vetores que acabou de definir.

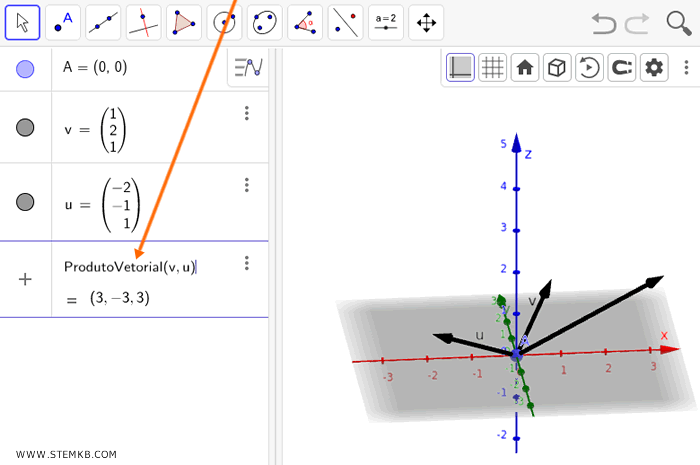
O Geogebra vai, então, calcular e exibir o produto vetorial dos seus vetores.

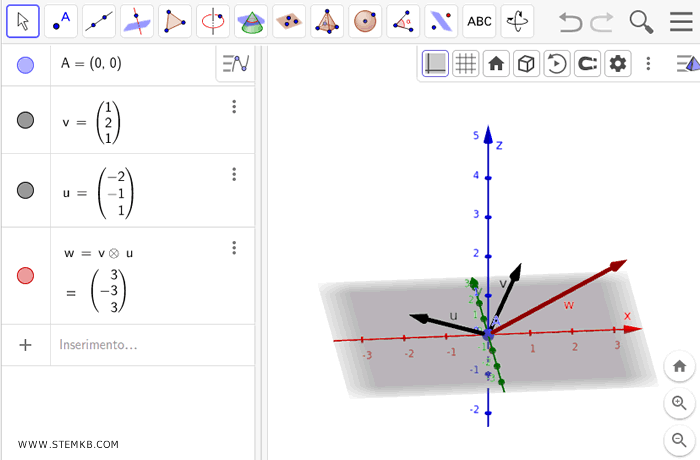
Neste exemplo específico, o produto vetorial resultante é o vetor w, com as seguintes coordenadas.

$$ \vec{u} = \begin{pmatrix} 3 \\ -3 \\ 3 \end{pmatrix} $$

A importância do produto vetorial reside no fato de que, ao calcular o produto vetorial entre dois vetores u e v, obtemos um terceiro vetor w, posicionado de maneira única e perpendicular aos vetores originais. A orientação desse vetor resultante é definida pela ordem dos vetores originais. Se os vetores iniciais estiverem alinhados na mesma direção, o resultado é um vetor nulo. A magnitude do produto vetorial é um indicativo da área coberta pelos dois vetores no plano que compartilham.

Aprecie este guia prático oferecido pelo StemKB e aguarde por mais novidades.